Un singe"destiné à la savane"[Dehaene] - Un enfant "destiné à la science"[Piaget]
"L'a priori ne SE PRESENTE sous forme de structures nécessaires qu'au terme de l'évolution des notions et non pas à leur début, [mais] il n'est pas question de réduire de la sorte le supérieur à l'inférieur. L'histoire des sciences montre que tout effort de déduction pour établir la continuité entre une discipline et une autre aboutit non pas à une réduction du supérieur à l'inférieur, mais à créer entre les deux termes un rapport de réciprocité ne détruisant nullement l'originalité du terme le plus élevé. [Pigaet NI9,14-15] C'est au terme et non pas au point de départ de l'évolution intellectuelle qu'il faut s'attendre à rencontrer les notions rationnelles exprimant réellement le fonctionnement"
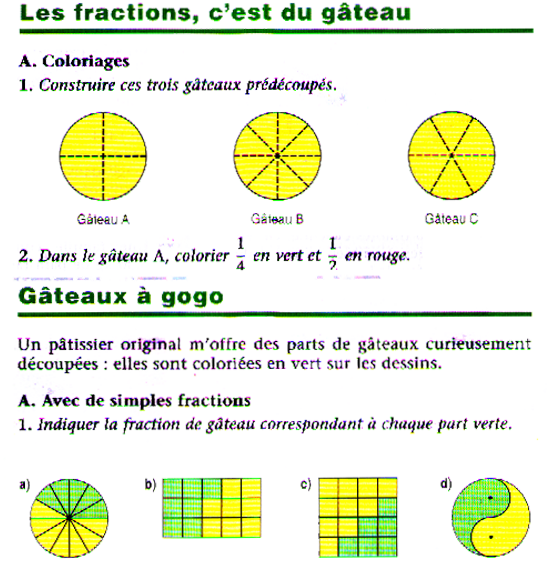
"Addition entre fractions ayant des dénominateurs égaux Supposons avoir une grandeur, par exemple un rectangle, et de la diviser en 9 parties égales. Considérons d’abord et ensuite du rectangle ; en tout nous aurons 5+2=7 parties égales à du rectangle. La fraction représente donc la somme de et . Nous pouvons écrire, donc, selon l’image :

Ce compte-rendu narratif et imaginatif est parfaitement calqué sur celui des petites balles : les expressions fractionnaires et sont avant tout reconduites aux nombres entiers 5 et 2, pour ainsi reproduire l’addition 5+2, imagée au travers de cinq-plus-deux petit rectangles, et cette image – indoutablement évidente en sa clarté absolue – est censée rendre compréhensible le fait opératoire de l’addition entre deux fractions. Le problème se pose lorsque avec cette même image évidente et claire, nous devons justifier le fait qu’au contraire de ce qu’il se passe pour le couple & , le couple & ne peut pas donner lieu à une addition directe entre ses deux termes. Les textes élémentaires soit ne disent rien à ce propos, en se bornant à donner l’instruction de reconduire les fractions involvées à un dénominateur commun, pour ensuite exécuter l’addition comme dans le cas des fractions ayant le même dénominateur, à savoir comme dans le cas d’une addition/entassement entre des entités entières. Mais il est au contraire sûr et certain que l’ image offerte témoigne d’ une vérité parfaitement en opposition avec cette impossibilité opératoire d’ additionner deux fractions ayant des dénominateurs différents.
Cette image traduit en GII l’addition entre deux fractions ayant différents dénominateurs selon la méthode adoptée jusqu’ici... mais elle rend incontournablement évident que si et sont deux petit rectangles entiers, faisant partie d’un rectangle plus grand (le rectangle « 1 »), alors ils sont autant parfaitement additionnable, que le sont & , ou & .
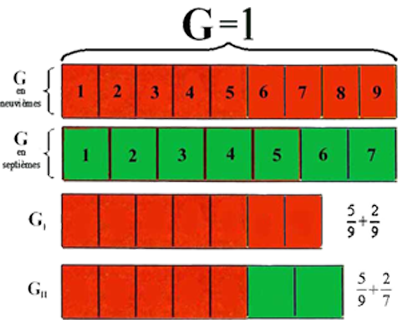
L’imagination qui nous témoigne de l’additionnabilité entre des « neuvièmes », nous témoigne ici et maintenant – dans la même image et pour les mêmes raisons – l’additionnabilité entre des « neuvièmes » et des « septièmes » :

L’imagination en GI témoigne avec évidence le phénomène arithmétique de l’addition entre deux fractions ayant un dénominateur égal : il est évident que les 5 rectangles rouges et le 2 rectangles célestes composent le rectangle unitaire GI ; mais cette même imagination témoigne avec la même force d’évidence que nous pouvons bien prendre directement les 2 rectangles vertes (plutôt que les 2 rectangles célestes) et les ajouter sans délai (avec la même immédiateté que dans le cas de GI).aux 5 rectangles rouges, en façonnant de la sorte le rectangle unitaire GII?GI . « Sans delai » signifie qu’il n’y a aucunement besoin d’intervenir sur les 5rouges + 2vertes rectangles à additionner (par exemple en les faisant préalablement devenir 63rouges/verts petits rectangles) pour pouvoir obtenir la somme GII qui manifestement se trouve déjà sous nos yeux. En semplifiant encore : il est clair que notre appréhension sensible/imaginative d’une quelconque quantité étendue ne pose aucun veto à aucun genre d’addition. Si un « septième » et un “neuvième” ne sont que deux des quadrilatères ci-dessus, alors leur accumulation ne pose aucun problème:

Il est clair pourtant que l’addition « » ne peut pas être réalisée avec autant d’immédiateté : les symboles cryptogrammatiques fractionnaires sont en toute évidence porteurs d’un quid qui nous empêche une synthèse immédiate entre les deux syntagmes en question. Le « blocage » de l’addition entre deux fractions ne se produit donc qu’au niveau irréductible de la présence symbolique des nombres, pour des raisons qui à présent nous échappent. A la différence tant de la somme (immédiatement faisable) entre les deux symboles 7 et 9, que de la synthèse perceptive des deux rectangles, la somme entre et ne peut être effectuée qu’ une fois opérée une préalable transformation de ce couple de syntagmes symboliques dans le couple .




Les quadrilatères Bi façonnés avec les triangles rectangles qui composent la Couronne Carrée (CC) jaune, varient tant de forme (le rapport de proportionnalité entre les côtés a et b) que de surface, tandis que les carrés c2 varient d’orientation et de surface, mais ils ne varient pas de forme. Or comme il s’agit d’un même mouvement de rotation d’une forme carrée c rigoureusement interne à un même carré KA , nous ne dirons pas que c2 0…. c2n … →∞ sont des carrés différents, mais qu’il s’agit des différentes expressions de la rotation d’un même carré à son intérieur.
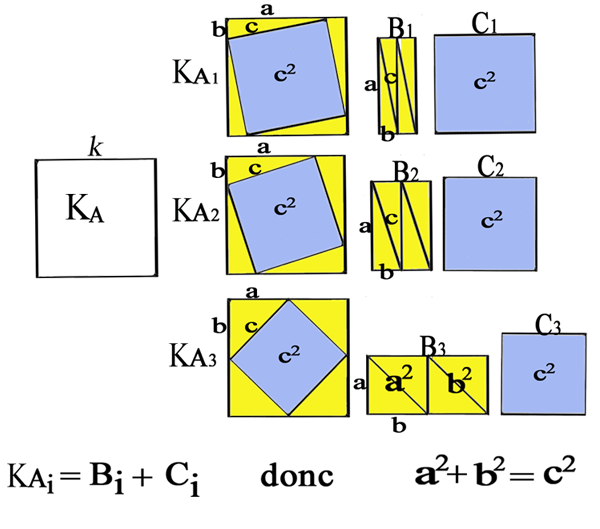
· Lepérimètre de la couronne carrée est inversement proportionnel à la surface de la couronne carrée.
La couronne carré CC est formée par deux périmètres :
le Périmètre Externe PE={a+b}+ {a+b}+{a+b}+{a+b} du carré KA, qui est toujours le même (et où {a+b} = kA, qui est le côté du carré-racine KA, à savoir de l’objet sous observation )
le Périmètre Interne PI={c+c+c+c} qui diminue au fur et à mesure que le rapport a/b se rapproche de 1 (à savoir que a tend à =b).
Nous voyons donc que le Périmètre Total PT =PE +PI de la couronne CC augmente au fur et à mesure que sa Surface diminue : PTCC=1/SCC.
Nous voyons donc que le Périmètre Total
Pour que cette vision perceptive se transforme en un théorème, nous devons la généraliser, ce qui revient à dire que le
passage généralisateur r(p/2) { ci2 = Bi
= ai2+bi2} ⇒
· Or si on regarde bien, le degré de certitude de l’ évidence perceptive du terme final r(p/2) est le même que dans le cas du terme initial r(p=0) , où a=c et b=0 [et dont l’évidence – toujours de surface – n’est pas perceptive mais projective]. Dans ce cas aussi, vaut l’équivalence a2+b2=c2.
La variation de
surface de Bi le long de la rotation/variation 0→p/2
de c2 résulte donc
comprise entre les deux extrêmes a=c
et a=b, pour lesquels vaut la
relation a2+b2= Bi = c2
. Ce qui demeure constant comme quantité absolue
au sein de cette
variation est a+b=kA,
c’est à dire la longueur extensive du côté de ce
carré KA
·
Nous avons donc placé notre terme moyen Bi=a2+b2 au deux
extrêmes r(p=0) r(p/2) de cette transformation, et nous
nous demandons de quel droit le
plaçons-nous partout (« pour n’importe quel degré ») au sein de la
rotation r(p=0)
→ r(p/2) du creux
ci à l’intérieur de KA .
La seule chose qui ne change pas le long de cette rotation est la longueur absolue de la somme a+b= kA car nous nous trouvons toujours à l’intérieur de KA.
Sur cette base, partons de r(p=0) où a2+b = c2 (car a=c et b=0). Le long du parcours r(p=0) a=c → r(p/2)a=b , a diminue, et b augmente, tandis que leur somme =kA reste constante. A chaque diminution extensive de a correspond donc une égale augmentation extensive de b.
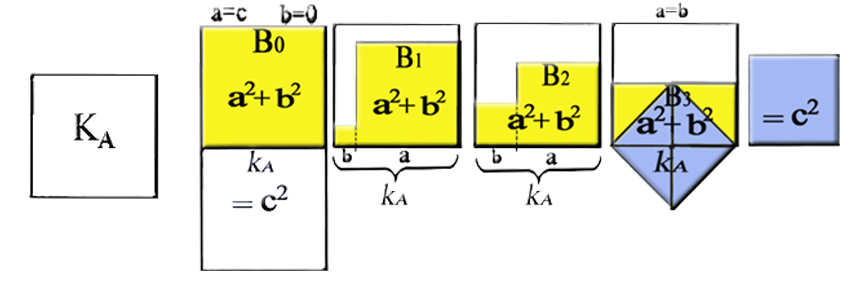
Nous pouvons en conséquence imaginer
que sur le même côté-racine kA
la surface totale du carré initial a02 (=c02)
se distribue sur les deux surfaces carrées ai2 et bi2
sans que jamais l’équivalence projective
initiale a02 +
b02= c02 (où a=c et b=0) ne subisse
la moindre variation jusqu’à sa finale manifestation perceptive, lorsque a=b
La certitude de ce théorème se fonde donc sur la permanence devant nous de ce carré KA et son extension individuelle absolue, et l’évidence finale de notre démonstration jaillit du fait que nous restons ancrés à la quantité absolue de la figure – cette figure – qui est le sujet logique individuel des transformations que nous contemplons à son intérieur, car tout le reste - les formes, les dimensions, les orientations et le surfaces - change incessamment devant nos yeux.
[SULL’INTRODUZIONE DEL NUMERO FRAZIONARIO] Se vogliamo risolvere problemi nei quali intervengono, oltre alle unità intere, anche parti dell’unità intera , siamo costretti considerare un nuovo ente , l’ente costituito da una coppia ordinata di numeri naturali, il secondo dei quali sia diverso da zero. Queste coppie ordinate di numeri naturali, pur rappresentando concettualmente enti molto diversi, sono state chiamate anch’esse numeri, e per distinguerli dai numeri naturali, alla parola numero si è aggiunto l’attributo frazionario. Il lettore non dovrà dunque dimenticare che quello che viene chiamato numero frazionario altro non è che una coppia ordinata di numeri naturali con il secondo numero diverso da zero.
[SULL’INTRODUZIONE DEL NUMERO IRRAZIONALE] Vogliamo far vedere come ancora esigenze di carattere pratico portino a dover considerare un certo insieme di enti. Per risolvere in generale il problema della misura dei segmenti si è costretti a introdurre un nuovo ente. l’ente costituito da una coppia di classi dinumeri razionali assoluti, e ad attribuire a questo nuovo ente il nome di numero; per distinguerlo poi dai numeri già noti, questo verrà chiamato numero irrazionale.
Al lettore può forse apparire strana l’idea di assumere come misura del segmento s rispetto ad u l’ente costituito da due classi di numeri razionali A e B. Ricordo però che la stessa situazione di disagio si è verificata quando per la prima volta si sono considerati problemi nei quali intervenivano, oltre alle unità intere, anche parti aliquote dell’unità intera, e dovevamo esprimere la soluzione di questi problemi con l’introduzione di un nuovo ente – il numero frazionario – costituito da una coppia ordinata di numeri naturali. [...] La confidenza che abbiamo con i numeri frazionari non ci deve lasciar sfuggire l’INTIMA ESSENZA di questi numeri. In altre parole, sia dato un insieme di enti di natura qualsiasi; questi enti sono chiamati numeri quando per essi si possono definire le quattro operazioni e le consuete proprietà. SI CHIAMA NUMERO qualunque ente, di qualunque natura, che presenti certe proprietà […] Esse definiscono L'ESSENZA DEL NUMERO.[G.Zwirner,Istituzioni di matematiche, Padova1975]
0. [« La general contemplazione del tutto » : saisie de la Totalité Evénementielle Globale] Avant de commencer notre enquête expérimentale, nous nous trouvons immergés dans la Totalité et confrontés à ses Lois . Cette Totalité se présente à notre esprit, ainsi qu’à l’esprit de Poincaré, comme ce galiléen « Corpo Perfettissimo del Mondo » que l’on ne que « l’on ne saurait séparer sans le mutiler », car « à la rigueur, il n’est pas jusqu’à l’attraction de Sirius qui n’agisse sur le pendule ». [VS45] Cette Totalité, chez Poincaré ainsi que chez Galilée, est l’espace/corps régit par le Nombre et l’Harmonie de Pythagore et sa Loi (1,2,3... à l'infini par Recurrence) et où l’unique vrai mouvement (« intégral» ou « pur » puisqu’il ne qui ne dépend pas de la relativité de nos choix conventionnels ni des conditions matérielles où il se déroule) est le mouvement circulaire : le Groupe de déplacement.
1.[Saisie empirique de la « formation événementielle » du Pendule] Au sein de cette Totalité, mon attention est attirée par celle qu’à ce stade nous pouvons appeler une simple « formation événementielle », qui pourrait se dissoudre tout de suite, ou se montrer solide comme un nouveau corps céleste au sein de notre Ciel scientifique. Ce pendule P oscille lentement devant moi : un fil F très long et subtil attaché en C se termine avec une lourde sphère S accrochée à son bout inférieur (P=CFS). A chaque fois que le pendule passe par l’extrême inférieur D de son mouvement, il touche une petite clochette qui sonne. Le mouvement périodique (T) de P est extrêmement constant: la durée des intervalles d’oscillation est toujours la même (k) .
2.[Saisie expérimentale du Pendule en tant totalité événementielle « solide » ] A) La lenteur hypnotisante du mouvement kT de P me frappe tellement que je me propose de l’accélérer : j’attrape donc la sphère, et je la pousse avec force vers les hauteurs. Résultat : j’accélère en effet – et beaucoup ! - la vitesse de la sphère … qui vole maintenant devant moi pour atteindre quasiment la hauteur du point où son fil est attaché. Mais dès qu’elle revient… et remonte pour revenir, je dois remarquer avec un grand étonnement, que je n’ai rien changé… ou du moins je n’ai rien changé de ce que je me proposais de changer, à savoir la rapidité du pendule, et non pas la vitesse de la sphère. B) Je décide alors de la ralentir . Je la rattrape au vol, et je l’arrête presque… Maintenant la vitesse de la sphère est extrêmement réduite… mais son espace de mouvement aussi… et le pendule oscille... toujours avec cette même fréquence ! C) Dernière tentative : je détache la sphère et je l’alourdis de dix fois : je me dis que cela devrait avoir un effet… mais rien ! Même rythme ! Manifestement, c’est le pendule qui a son oscillation, en tant que totalité insécable, car si ce n’était qu’une sphère sans fil, j’aurais produit, avec mes interventions, seulement l’accélération/ralentissement qu’en effet je souhaitais, tandis que sans m’y attendre j’ai obtenu qu’à côté de ces mêmes changements l’identité de ce kT se détache encore mieux sur leur fond hétérogène; par contre, le fil sans la sphère n’est qu’une corde irrégulièrement ondoyante .
3.[Saisi mathématique de la Fréquence comme ratio temporelle interne, solidaire à tout pendule donné] Je me rends compte, donc, qu’avec « rapidité de mouvement » j’entendais en réalité deux choses : d’un côté la rapidité de déplacement de cette même sphère sur son arc d’oscillation, et de l’autre côté la rapidité de sa fréquence d’oscillation : combien de fois-par-unité-de-temps S passe par le point D. C’est donc cette fréquence f que je ciblais en ciblant ce pendule et son mouvement régulier, même si je n’aurais jamais songé à une telle solide fixité : une certaine fréquence semble vraiment clouée au pendule dont elle est la fréquence. Or en tant que « fois-par-unité-de-temps » ou « fois par fois », la fréquence n’a strictement rien à faire avec la vitesse en tant qu’ « espace-par-unité-de-temps » car dans un cas il s’agit d’une durée entre deux temps (= événements ) et de l’autre d’une durée entre deux espaces (= lieux). Ceci est clair dans l’expression f = k × T , où « k » signifie irréductiblement l’égalité de durée qui lie deux périodes « T », et « T » n’est pas tout à fait une quantité d’ espace parcouru (car le pendule en parcourt de moins en moins, où que je le pousse dans l’espace circonstant, tandis que T reste identique) mais un certain mouvement unitaire et globale qui s’achève à chaque fois devant moi avec autant de clarté que devant moi s’achève le cercle – = périodos – que je viens de réaliser avec mon compas pour représenter l’arc d’oscillation de ce pendule. J’ai remarqué ce pendule donc (= ce pendule se fait retrancher au sein de la Totalité des événements) car il est l’étincelante présence d’un mouvement périodique dont les cycles de temps qu’il trace dans le temps sont toujours (de fois en fois) égaux entre eux ; j’aurais voulu le changer, comme si ce n’était qu’un mouvement parmi les autres… mais le pendule m’a répondu avec une étonnante obstination qu’il a sa fréquence à lui, aussi solidement ancrée à sa simple existence, que l’est la solidité matérielle de ses parties.
4.[Saisie génétique du pendule comme expression de la présence d’un corps qui tourne] A)Je me demande alors comment puis-je faire pour obtenir un changement de cette fréquence car il est clair désormais que dès que j’ai un pendule, j’ai en tous les cas une certaine fréquence, à savoir un certain cercle temporel de mouvement. Autrement dit : au sein de ce pendule que j’ai devant moi, je me demande quel est le facteur responsable de cette puissance d’égalisation interne dont il est doué (et donc de la cohésion de ce « solide événementiel » mécanico/cinématique qu’est le pendule) et qui fait que chaque fois que j’interviens pour modifier un paramètre au sein su système FCS, le pendule se rééquilibre et sa fréquence en résulte immodifiée. Je raccourcis les arcs, et il ralentit la vitesse, je rallonge les arcs, et il l’augmente…. B) J’ai une idée : j’agirai non pas sur la sphère S mais sur le fil F. Je l’attrape donc… et immédiatement – sous mes mains – la sphère subit une accélération. Finalement je comprends : je réessaye, et je vois que le plus je raccourcis le fil, les plus j’accélère la fréquence de l’oscillation. Donc la fréquence d’oscillation – la « voix » immodifiable de ce pendule – change en fonction de la longueur du fil. C) Mais qu’est ce donc que la « longueur du fil » au sein de cette totalité mécanico/cinématique (le tout insécable CFS de ce pendule, internement doué du soilde insécable et non spatial de son période T ) qui paraissait imperméable à toute intervention de l’extérieur ? Est-ce la longueur du fil la distance externe de CFS du centre de la terre, comme c’est le cas, par exemple, de l’accélération dans la chute gravitationnelle ? (En effet le pendule chute pour rejoindre la clochette en D…). La réponse est non : je peux neutraliser le facteur distance-du-centre-de-la terre, en faisant tourner comme une fronde la sphère S sur un plan de circulation parallèle et non pas orthogonal au sol. Dans ce cas aussi si je raccourcis le fil F j’obtiens ce même effet d’accélérer la fréquence du mouvement périodique de S. Conclusion : il s’agit d’une distance interne entre le centre C et la circonférence où bouge S, et dont le fil F est le rayon de ce cercle d’oscillation/circulation (pendule/fronde). La fréquence du mouvement de S change donc en fonction de la distance entre S et le centre C, c'est-à-dire e fonction de l’extension matérielle de ce même cercle (et non pas de l’extension circulaire en radiants des arcs parcourus). Ce pendule avec sa fréquence manifeste donc le cercle matériel d’appartenance commune de ses parties. C’est donc ce cercle en sa grandeur extensive réelle le « facteur d’égalisation » que je cherchais : si j’agis sur son rayon en en changeant la mesure absolue, j’agis sur la fréquence interne de ses mouvements : qu’il s’agisse d’un pendule, d’une fronde, ou d’une toupie… D) Qu’est ce finalement que ce « cercle matériel» ? C’est un général le cercle de rotation d’un corps ou d’un système de corps suffisamment solidaires entre eux qu’ils puissent participer d’une rotation commune, et de son péri-hodos. Je peux en effet bien faire du centre C où le fil F est attaché le centre de rotation d’un corps dont le « moment de rotation » tau - la force qu’il dégage par le fait qu’il tourne autour de son propre centre de rotation – augmente au fur et à mesure qu’on s’approche de ce même centre, et pour cette raison le mouvement en résulte accéléré.
Conclusion : ce pendule qui comme insécable totalité oscille devant moi, exprime au travers de la fréquence constante (kT) de ses propres oscillations - sa propre voix - la périodicité qui appartient à toute forme de rotation.
