En quête de métamorphoses naturelles (de la chenille au papillon) les enfants trouveront certainement des phénomènes qu'ordinairement l'on ne considère pas comme des «métamorphoses», comme par exemple le jaune de l'œuf qui se transforme en poussin.

Grâce à des évidences aussi immédiates et fabuleuses nous dirigerons donc l’attention sur l’universalité naturelle de la Métamorphose, qui se transforme ainsi en… Transformation.

Nous attirons maintenant l’attention de l’enfant sur le fait qu’il sait distinguer entre une orange et une pêche ou une pomme, mais qu’à partir de l'orange, ou de la pomme, pourtant si connues et familières... il ne sait aucunement reconnaitre un oranger ou un pommier, et d'autant moins «la graine d'un oranger, malgré que la graine, le fruit, la feuille, et la fleur… ne soient que les parties d’un même arbre.

De cette même façon, l’enfant se rendra compte qu'il sait distinguer la caille et le pigeon, mais qu’il ne sait pas remonter de la caille à l’œuf de la caille, en le distinguant de celui du pigeon. On lui montrera donc le monde comme une suite inépuisable de formes naturelles, tout à fait hétérogènes les unes par rapport aux autres, mais qui se fondent harmonieusement au sein d’un seule et même être vivant. Cette double prise de conscience distille enfin, dans l'esprit de l'enfant, les deux directrices dimensionnelles qui pulsent au cœur de l'univers qui l'entoure:

A) UNE DIRECTRICE VERTICALE de l'ordre naturel, suivant laquelle les choses ne se ressemblent pas - graine-racines-tronc/branches-fleur-fruit - mais qui sont puissamment unifiées par l'évidence, d'autant plus forte, que leur lien transformatif et logique: la feuille ne ressemble pas à la branche, la fleur ne ressemble pas à la feuille, et le fruit ne ressemble pas à la fleur... cela pourtant ne fait pas du fruit une "métamorphose" de la feuille, mais une transformation naturelle, car il s'agit des phases d'une même vie d'un même arbre;

B) UNE DIRECTRICE HORIZONTALE de l'ordre naturel, suivant laquelle les choses se ressemblent: tous les graines, toutes les racines, tous les troncs, toutes les branches et toutes les feuilles se ressemblent entre elles, abyssalement plus qu'une feuille ressemble à une branche ou à une fleur... L'enfant au marché distingue immédiatement le banc des fruits par rapport à celui du fleuriste, mais chez le fleuriste il y a les fleurs du pêcher, tandis que les pêches se trouvent ailleurs, et elles ont la forme d'une sphère, qui n'a rien de commun avec la forme des fleurs etc.

Cette table représente les deux directrices logiques parcourues non seulement par les phénomènes du monde, mais par l’esprit humain lui-même, en sa « théorie des ensembles » naturelle et spontanée, et nous avons ainsi atteint le cœur du programme pour l’Ecole Primaire . Arrêtons nous donc pour un commentaire sur ce schéma. Nous commençons par des considérations gnoséologiques et historiques, pour parvenir ensuite à leur conséquences didactiques:

LA TABLE de PITAGORE de la TRANSFORMATION :
redonner une Logique au nombre, e un Sens aux « ensembles ».

La notion mathématique d’ensemble/classe est née du sein d’une reconsidération purement logique du nombre, élaborée par Dedekind/Cantor/Frege afin d’émanciper l’arithmétique – et avec elle toute la science – tant de l’emprise de la « pensée aggrégative » qui pense aux unités numériques (monades, Eins…) comme à du sable ou des graines de quartz (Frege^[1A]) que de la pensée prélogique et imaginative d’une extension numérique (comme ) géométriquement justifiée. Pour les fondateurs de la perspective ensembliste en outre, le pire – le fait « honteux » pour Frege et « révoltant » pour Dedekind était que le simple manque de tout rigueur effectivement mathématique dans les définitions fondamentales soit constamment dédouané et justifié sur la base d’ « exigences d’ordre didactique » ^[1B]). Malheureusement, et comme si tout cela n’avait pas été dit et dénoncé par les créateurs mêmes des ensembles, des classes et tes ellipsoïdes purement logiques destinés à en donner une représentation imaginative [John Venn,1880]:

1) quant aux nombres, les pré/a-logique graines de sable de la « pensée agrégative » remplissent maintenant – sur les textes de mathématique élémentaire des simples cercles coloriés, en l’occurrence « vides », tandis que la ligne de fraction et la « ligne des nombres » sont ordinairement découpés avec les ciseaux ou avec le couteau pour les gâteaux.

2) quant aux concepts, des agrégats de choses sont réunis selon des attributs parfaitement dépourvus des seuls traits quantitatifs et arithmétiques intéressants du point de vue de la théorie des ensembles.

Or cette séparation complète entre classification logique et compte/mesure numérique rend tout à fait impossible:

1) Comprendre qu’est ce que c’est le 0 (puissance zéro, grandeurs négatives etc.) en ce qu’un zero purement logique (et donc en réalité pré-logique) signifie que dans les cercles coloriés il n’y a ni des petits poissons ni des petites sphères, et un petit poisson négatif ou une « – petite sphère » sont des choses dépourvues de sens.

2) Comprendre qu’est ce qu’une fraction , du moment que si diviser des nombres signifie couper des gâteaux, et que la fraction est une division, alors on ne comprend pas pourquoi une ligne de fraction entre deux nombres rationaux peut donner comme résultat un nombre rationnel plus grand que le nombre de départ (et vice-versa : multiplier deux fractions peut diminuer la quantité numérique de départ).

3) Comprendre qu’est ce qu’une grandeur incommensurable , car l’idée qu’étant donné un – « 1 » – gâteau et un certain nombre de personnes nous ne pourrons pas trouver un couteau suffisamment précis pour donner à chacune d’elle une tranche égale aux autres est tout simplement fausse, tandis qu’imaginer qu’étant donné deux segments de longueurs différentes – et donc un segment et une des ses parties – nous ne pourrons pas trouver un troisième segment suffisamment petit pour les mesurer avec exactitude est une idée strictement impensable.

L’alternative à cette catastrophe pédagogique existe : se servir effectivement des outils logiques/épistémologiques que ces mêmes Cantor, Dedekind, Frege, Venn ont créés lorsque, pour aider la compréhension directement mathématique du nombre, ont façonné l’outillage symbolique et opératoire dont les textes actuels n’arrêtent pas de se servir.

Si badi che parlo qui di strumenti per la didattica!, non del recupero del programma logicista, che resta un obiettivo prioritario della ricerca in Eironeia.

Per farmi intendere su questo punto delle due direttrici logiche (somiglianza orizzontale e differenza verticale) della nostra "insiemistica naturale" - e dunque sul fondamento effettivo della mia tavola pitagorica della trasformazione - consedererò ora un esempio analogo a quello della potenza zero, esaminato nella pagina sull' Offerta Formativa.

"Denominare" significa dare un nome.
"Comun denominare" significa dare lo stesso nome.

Se il numero naturale anti-fregeano ha più o meno sempre l'aspetto di una pallina colorata, la frazione anti-dedekindiana ha - superata la fase 0 della torta e attinto il primo passo verso il numero razionale - l'aspetto di una figura geometrica, in genere quadrati/rettangoli o cerchi:

Il secondo passo è l'introduzione dell' addizione tra due frazioni con lo stesso denominatore:

Il terzo passo è l'introduzione dell'addizione tra due frazioni con differente denominatore,poniamo 5/9+2/7. In questo caso l'alunno deve imparare a ricondurre le due frazioni a un comune denominatore, e cioè a passare per una fase intermedia (qui sotto segnalata dal giallo nella regione tratteggiata in rosso) che non è presente nel caso di frazioni con lo stesso denominatore:

Ora, nel mondo degli anti-dedekindiani numeri/grandezza, la necessità di questa riconduzione dei "noni" e dei "settimi" a dei "sessantatreesimi" è perfettamente incomprensibile - tanto quanto è incomprensibile la potenza zero se i numeri sono grani di sabbia e lo zero è un cerchio senza sabbia dentro.

Rappresentiamo infatti l'espressione "settimi", col rettangolo utilizzato nel caso dell'espressione "noni" (con "NG" intendo il numero/grandezza pre-dedekindiano):

Su questa base immaginativa, addizioniamo 5/9 e 2/7:

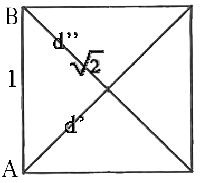
Ecco fatto!. Gli occhi dell'alunno vedono l'evidenza di UNA grandezza totale verde e rossa, che per esistere come somma davanti ai nostri occhi e al nostro intendimento non ha alcun bisogno di passare per una ri-denominazione dei suoi componenti. In un colpo solo abbiamo dunque 1) addizionato il razionale/grandezza NG' denominato "settimi" e il razionale/grandezza NG'' denominato "noni", senza alcun bisogno di ri-battezzare entrambi come "sessantatreesimi"; 2) fatto finta che l'immensa fatica di Simone Stevino e Richard Dedekind non sia mai esistita; 3) abbandonato noi stessi e l'alunno nel non-luogo di una pseudo-comprensione che gli e ci si abbatterà contro nel momento in cui, per far capire il senso di dovremo spiegargli che nel "quadrato di lato unitario" NG=1 i cui due estremi (=parti) AB coincidono con gli estremi (=parti) delle due diagonali d' e d'', questo stesso lato e queste stesse diagonali non sono "divisi" né dal numero 1, né dalle loro parti coincidenti all'interno del quadrato in questione, e che questo è il senso del simbolo . Nel mondo dei numeri/grandezza/grani-di-sabbia - in cui i numeri non hanno logica e la logica non ha né segno ( + o -) né 0 - tutto questo non ha nessun senso, e quello che ci resta tra le mani sono simboli (non "insiemi") vuoti, e cioè segni oscuri quanto solo possono esserlo 0 pescioluni rossi in un acquario senz'acqua.

L'alternativa didattica c'è, e la mia tavola pitagorica della trasformazione ne è un'espressione chiara. Se ridiamo senso alle parole utilizzate dall'inizio, possiamo ricomnciare da "divisione", che nell'etimo è di-visione, e nel greco matematico è "diaïresis" [airéo=scelgo].

In entrambi i casi, per duplicare la nostra visione/idea [v-ideo], al suo interno tra-scegliendo due invece che uno [1 = l'idea stessa come totalità indistinta, alla sua 1^a apparizione]... "attraversando" l'ambiente dove l'abbiamo rinvenuta [dove di- è "dia", come in "dia-logo" o "dia-fano"] non c'è bisogno di segare e frammentare nè linee geometriche né torte né pani dispari, perché si tratta di un traslato attraversare con la nostra mente lo spazio puramente logico di una identità di genere, resa in se stessa tras-parente [dia-fana] dalla nostra lente intellettuale che - come al mare con maschera e boccaio - ci permette di percepire il fondo attraverso il contatto con la superficie.

La "diairesis" è infatti per i greci il procedimento di istituire una "dif-ferenza specifica" [la dia-phorà, che in Dedekind è la Verschiedenheit colta dal nostro spirito, che opera dunque quella Einteilung - partizione interna puramente matematica, chiamata Scnhitt: "taglio" ]... nel seno di una identità generica, secondo il rapporto logico genere/specie proprio di qualunque composto definitorio.

Ci sono gli alberi (genere) e gli aranci (specie), ed è certo che non possiamo segare e frammentare in pezzi l'Albero, se vogliamo ottenere un Arancio, anche se è vero che il genus Albero si "sub-divide" - dia-forizza, differenzia... - in specie. Ora i bambini sanno benissimo che non possiamo sommare metri e chili, perché sarebbe come sommare mele e arance: e questa è la prima conseguenza aritmetica della scelta logica di enumerare gli oggetti nella linea 2 della nostra tavola, denominandoli dif-ferentemente, e cioè verticalmente, "arancia", "mela", "ciliegia" etc. Potremmo comun-denominarli orizzontalmente "frutta" e allora avremmo 5 frutti - ma finché decidiamo di denominarli secondo la loro differenza specifica - e cioè tenendoli ben stretti appesi al loro proprio albero di provenienza - ... non potremo sommarli tra loro, perché è così che abbiamo deciso.

Il bambino questo lo capisce perfettamente: basta tenergli a mente che i NUMeri son NOMi, e che quando c'è un nome c'è sempre un COG-NOME. Così, come lui e chiunque altro ha un NOME che è solo suo - per cui non potremo mai dire: "ecco i signori Fabrizio" (fa ridere!) - ma ce ne ha pure un altro - il CON-NOME in comune coi suoi familiari, per cui possiamo dire "ecco i signori Rossi" (come i pesciolini)... allo stesso modo ogni numero/frazione ha un con-nome, che si mette su, e si chiama numeratore, e un nome, che si mette giù a de-nominare il numero, e per questo si chiama de-nominatore, e fa la differenza tra la frazione da lui denominata e tutti gli altri numeri/frazione che non portano il suo stesso nome scritto in basso. Dunque, quando il de-nominatore che fa-la-differenza neanche è presente, allora quello è un numero che può formare una famiglia con qualunque altro numero che pure lui non fa la differenza: i grandi dicono che n+m=x "ha una soluzione" per qualunque numero "naturale". Ora, con la stessa immediatezza con cui sa che "i signori Fabrizio" fa ridere mentre "i signori Rossi" no, il bambino sa anche che basta de-nominare differentemente una ciliegia, per poterla considerare dentro la stessa famiglia delle pesche e delle arance etc. ottenendo così la famiglia dei signori Frutta che lui conosce benissimo, dove il cognome "Frutta" non è un ammasso di materia da tagliare, nè un frullato di cose da mischiare, ma semplicemente il nome di un insieme di cose molto buone da mangiare, che ci permette di poterle trovare tutte raccolte insieme al mercato quando ci andiamo con la mamma.

Questa possibilità (=POTENZA) sempre aperta di dare uno stesso nome - come "SESSANTATREESIMI" - a due numeri differentemente de-nominati, come il signor n SETTIMI e il signor m NONI è la Magia del Numero, e questa magia, che permette di mettere in una stessa famiglia due numeri con nomi diversi come se potessimo trasformare un pesca in un'arancia a nostro piacimento, si fa con la tecnica del comune "multiplo", e cioè "moltiplicando" i due nomi non sommabili (perché stanno sotto e fanno la differenza!) p=7 e q=9 così da ottenere il BI-NOME pq, per gli amici 63. E così, grazie al (da noi!) PRODOTTO nome logico/aritmetico 63, de-nominatore nuovo di zecca dei signori n/7 e m/9, adesso possiamo unirli in una SOMMA.

Che esperienza ha fatto il bambino in questo modo? ha fatto l'esperienza della sua potenza di de-nominare quello che ha davanti, secondo la sua scelta di classificazione.

Lo zero di questa tavola pitagorica della trasformazione è dunque infine il bambino stesso, e la sua capacità di viaggiare in verticale e in orizzontale, lungo le somiglianze e le differenze che via via scoprirà nella sua esplorazione del mondo.

Nelle nostre lezioni, questa potenza verrà esercitata con consapevolezza, tanto in verticale e in orizzontale. Si sensibilizzeranno così i bambini a questi due ordini naturali del mondo: l'ordine verticale è quello dell'identità propria - della "differenza specifica" - degli esseri viventi, che in se stessi hanno la potenza di riunire ("produrre" e ri-produrre) forme tra loro del tutto eterogenee; mentre l'ordine orizzontale, analogico e corale, è quello in cui tutto quello che esiste mostra di partecipare all'unità e all'armonia di una sola Natura.

I bambini raccoglieranno esempi, e riempiranno la loro "tavola pitagorica" delle forme del mondo, e delle creature che in sè le riuniscono, per far sentire attraverso di esse la propria inconfondibile (= incommensurabile!) voce.

4. Il ciclo degli elementi e l’avvicendarsi delle forme.

Su questa base narrativa ora risvegliata, si racconta il ciclo degli elementi : come si forma una goccia d’acqua in mezzo all’aria? (condensazione della pioggia)… e come si forma una bolla d’aria in mezzo all’acqua (ebollizione, o bollicine frizzanti che nascono dal nulla in fondo al bicchiere…). L’attenzione è innanzitutto su queste storie… che il bambino al momento si limita ad ascoltare, ma le storie sono raccontate in parallelo analogico: un goccia d’acqua che piove sulla superficie dello stagno, è sferica come la bolla d’aria creata dalla rana in apnea: l’una cade dal cielo, l’altra sale dal fondo… sulla stessa superficie.

Piovono gocce d’aria sul tetto dell'acqua, o si posano bolle d’acqua sul fondo dell’aria?

L’attenzione si allarga via via alle forme della natura: le onde nello stagno si espandono concentriche una dopo l’altra dallo stesso centro, così come fanno i cerchi che di anno in anno segnano l’espandersi dell’albero caduto un giorno, come seme, nello stagno della terra… e che da allora sale come un vortice, allungandosi... come la fiamma di una candela… distendendosi... come l'eclittica di un sistema solare nello spazio cosmico.

Le stesse forme giocano e danzano come in una festa infinita… e il bimbo gioca con loro e le vede danzare: sull'orizzontale armonica del loro coro, e sulla verticale della loro unica e inimitabile voce solista….

III. TEMPORALIZZARE.

[Discipline coinvolte: Italiano e Scienze]

1. Le FASI

Quello che caratterizza le Trasformazioni rispetto alle Metamorfosi, è un ordine narrativo di sviluppo secondo fasi. Il ciocco di legno non è una fase naturale di sviluppo del bimbo Pinocchio, come non lo è l’asino: le Metamorfosi giustappongono magicamente forme naturali (la verità del loro susseguirsi è unicamente profonda, incantata e narrativa) mentre le Trasformazioni fanno susseguire le forme (per quanto eterogenee) secondo un ordine naturale di sviluppo, universalmente riconoscibile.

Ci si concentra ora su questa direttrice verticale naturale, analogicamente proiettata sul tutto l’universo conosciuto dal bimbo: il cucciolo del gatto, del fiore, dell'uomo, di Dio...dicono tutti, inequivocabilmente e con la stessa chiarezza, che per venire alla luce bisogna cominciare...

La stessa cosa vale per il ciclo degli elementi. Quando la goccia si forma in cielo per condensazione, appare tutta insieme in un solo istante, oppure c’è un tempo di formazione? Te lo immagini questo tempo? Per esempio, quando si dice: "sta per piovere"… cosa immagini che accade nel posto in cui – come le bollicine nell’aranciata – cominciano a formarsi le gocce d’acqua? E cosa pensi che succede da quando accendi il fuoco sotto la pentola, e dopo un po’ si creano le bolle? Osserva: si creano subito già fatte, o succede qualcosa prima? E anche in questo caso, lo sapresti dire "sta per bollire"? E da cosa te ne accorgi?

2. La Potenza/Atto

Il narrativo e naturale susseguirsi secondo fasi di qualunque cosa viva nel mondo, distilla nell’animo del bambino la doppia polarità della potenza e dell’atto.

La sensibilizzazione al tempo interno di ogni processo secondo un incipit germinale (sta per piovere, sta per bollire) e la piena manifestazione di quello che così si annuncia, fa infine ben intendere al bambino che una forma manifesta – per esempio un uovo – non è solo ciò che attualmente essa è, perché allo stesso tempo è la potenza di qualcosa: si insegnerà allora a saper dire non che "nell’uovo" c’è il pulcino (altrimenti come ti potresti fare l’uovo al tegamino?), e neanche che a un certo punto così d’un tratto nasce un pulcino dall’uovo, ma che dentro l’uovo avviene una trasformazione che prende del tempo, e che dunque l’uovo porta in sé la potenza di questa trasformazione (e cioè l'uovo è un pulcino in potenza), per attualizzare la quale serve il calore, così come serve acqua, aria e sole perché nella terra il seme di trasformi in pianta, e serve l’educazione perché un bimbo si trasformi in uomo.

3. Il Tempo

[Discipline coinvolte: Italiano, Religione, Scienze]

Chi sa raccontare, sa anche contare.

Mostriamo ora al bambino che lui sa già contare i tempi del mondo. Abbiamo a questo punto già risvegliato in lui un senso del tempo naturale più profondo e comprensibile di quello dell’orologio: per fare un albero ci vuole un fiore… e ci vuole tempo.La goccia d’acqua in cielo ha i suoi tempi per condensarsi, e cosi il pulcino nell’uovo… Niente viene fuori tutto insieme: neanche Dio, che pure lui è arrivato tra noi come qualsiasi altro cucciolo.

E allora, chiediamo al bambino: li sappiamo contare i tempi delle cose?

Quanti tempi, per esempio, per UN uomo? - DUE!:da piccolo e da grande... TRE! - Bambino, adulto e vecchio... QUATTRO! - Bambino, giovane, adulto e vecchio...CINQUE! - Neonato, bambino, giovane, adulto e vecchio... SEI! - Nella pancia della mamma, neonato, bambino, giovane, adulto e vecchio... SETTE! - Nella pancia della mamma, neonato, bambino, adolescente, giovane, adulto e vecchio...

E UN albero? Quanti tempi ha? DUE! - Seme e albero...TRE! - Seme, pianta e albero...QUATTRO! - Seme, pianta, albero, foglie...CINQUE! - Seme, pianta, albero, foglie, fiori…

Si insegna così al bambino a contare – e dunque a sentire – i tempi naturali delle cose che lo circondano, e sul fondo, dunque, unico e coerente, silenziosamente uno per tutte, il TEMPO .

IV. MISURARE

[Discipline coinvolte : Scienze, Musica, Tecnologia, Matematica]

1. Battere il tempo: la Musica.

Il solfeggio naturale degli alberi, e la musica in classe.

Una volta che il bambino ha sentito e capito che la vita del mondo e delle creature che lo abitano si svolge nel tempo, non in astratto - sulla "linea del tempo" - ma perché ogni cosa ha il suo tempo possiamo porre la domanda: "e ora che sapete contare i tempi degli alberi e delle stagioni, dei pulcini e degli uomini, della condensazione e della rarefazione… lo sapreste contare il Tempo, da solo – il tempo comune a tutte le creature – così come fate per i tempi delle singole creature e dei singoli fenomeni?"

" ... "

"Non avete capito la domanda? Diciamo così allora: se questa è un’arancia, tu sei sicuro che perché si formasse abbiamo dovuto aspettare una serie di tempi: 1) il seme piantato nella terra, 2) la pianticella che cresce; 3) l’albero maturo; 4) il tempo dei fiori; 5) il tempo delle foglie; 6) il tempo della nascita dei frutti; 7) il tempo della maturazione dei frutti. Almeno sette tempi:OK?"

"Sì!"

"Noi sappiamo quindi che l’albero sa contare i suoi propri tempi, e a tempo dovuto dà i fiori, le foglie, i frutti… E infatti gli alberi tagliati vengono usati dall’uomo per misurare il tempo: si contano i cerchi dei grandi alberi secolari , e si giudica così in che epoca sono stati piantati. Insomma... tante creature sanno naturalmente misurare il loro proprio tempo. OK?"

"OK!"

"Adesso rifaccio la domanda: lo conoscete un modo per contare i tempi dentro il Tempo, in modo che possiate dire con certezza: "ne è passato del Tempo!: sono passati tre, quattro, cinque tempi… dall'istante in cui ho cominciato a contare!" ?..."

"L’OROLOGIO!"

"Bravi! L’orologio - TIC-TAC-TIC-TAC… batte il tempo! Va bene…. ma mica l’albero c’ha l’orologio per saper fare i fiori a tempo debito! Oppure ce l'ha nel panciotto?"

"MA NO!"

" E allora io vi chiedo: senza orologio, voi lo sapete fare quello che fa l'albero? Sapete tenere il conto del tempo?"

Arriviamo così alla MUSICA.

Il bambino capisce che – calendario e orologio a parte – lui stesso ha , come gli alberi e i pulcini – il senso del tempo e della durata. Gli si fa vedere che se si impegna, sa far durare una stessa canzone sempre lo stesso tempo, anche senza orologio. Ma la musica non è solo ritmo: la melodia e l’armonia sono capaci di far sentire un inizio, prevedere una fine, ascoltare una pausa. Si ascolterà allora la musica mostrando che in questo modo si ascolta il modo in cui il tempo scorre e viene misurato secondo fasi, e secondo potenza/atto.

2. Far battere il tempo: il Pendolo.

A questo punto si chiede come fa l’orologio a battere dei tempi sempre uguali, e si introduce il PENDOLO come fenomeno fisico, l’OROLOGIO A PENDOLO come strumento di misura del tempo, e il METRONOMO come strumento di misura della musica. Si mostra che il pendolo oscilla sempre con la stessa frequenza, qualunque cosa succeda, perché la frequenza resta la stessa a prescindere da ampiezza e velocità di spostamento della sfera oscillante.

Una volta capito l’ISOCRONSMO, si fa capire la differenza tra una clessidra e un pendolo: se urti la clessidra disturbi la sua capacità di misurare, mentre se urti un pendolo no.

Si fa costruire un pendolo, e si mostra il funzionamento del metronomo e dell’orologio a pendolo. Si fa capire la relazione tra rotazione della terra e la regolarità del pendolo come fenomeno di caduta sulla Terra.

V. CONTARE

[discipline coinvolte: Matematica, Scienze, Musica]

Siamo infine arrivati al NUMERO.

Il mondo del bambino è ora popolato di metamorfosi, trasformazioni, fasi e tempi, sviluppi, processi, ritmi e storie... e il bambino ha in più già enumerato tutto questo - "1: un seme! 2: una pianticella!… 3: un albero!… 4: un frutto!..." - ha sentito il solfeggio naturale del mondo, e ha esercitato il solfeggio musicale cantando o battendo il ritmo...

Possiamo allora servirci di tutto quello che ora il bambino sa e sente per parlare della successione 1,2,3,… non in termini di palline o oggetti da accumulare (e dunque non come 1+1+1…), nè di una semplice linea geometrica, ma in termini di fasi di sviluppo e fenomeni di trasformazione. I numeri, che fino ad ora ci sono serviti per enumerare le fasi vitali dei fenomeni che ci circondano (numeri numeranti), vengono visti essi stessi non come sassolini o semplici strumenti, ma come partecipanti (numeri numerati) a quegli stessi fenomeni di vita, sviluppo e trasformazione.

In più, i numeri sono ora pronti ad essere NOMI: nomi magici e potenti, che possono dare una famiglia nuova - una nuova denominazione - a qualunque cosa incontriamo nel mondo o ci venga nella mente...

Quando infine apparirà il seme dello zero, avrà dunque un aspetto del tutto diverso da un semplice e inerte nulla in cui non c'è niente da accatastare: il bimbo avrà già sentito e nel suo cuore saputo che quel cerchietto vuoto non è che la voce della sua più vera libertà di apprendere, e dunque di creare.

VI. CALCOLARE

[discipline coinvolte: Matematica, Scienze]

OBIETTIVO GENERALE: la continuità di senso nell’apprendimento della matematica lungo l'interezza del primo/secondo ciclo dell’educazione.

Strumenti pedagogici: agire sulla pre-comprensione dei simboli numerici e dei loro comportamenti operatori, in modo che fin dall’inizio l’allievo non percepisca aggregati di cose dello spazio ma processi logicamente identificati che si svolgono nel tempo.

Strumenti didattici: non parlare più di "quattro" operazioni alla scuola primaria, per poi aggiungere una "quinta" operazione – la potenza – e la sua inversa, la radice – nel biennio della secondaria, dotate di "proprietà" senza nome. Bensì: parlare fin da subito e simultaneamente di TRE operazioni – Potenza, Prodotto, Somma – e delle loro inverse – Radice, Divisione, Sottrazione – così come in Geometria si parla fin da subito delle TRE dimensioni dello Spazio (anche se la stereometria appartiene a una fase successiva a quella della geometria piana) mostrando come quelle stesse proprietà della potenza-prodotto-somma si trasformano le une nelle altre col passare di dimensione in dimensione, pur mantenendo il loro senso logicamente unitario e operatoriamente univoco.

Primo passo. La logica d'uso dei simboli: Il Numero-Potenza, il Prodotto, la Somma.

Agire allo stesso tempo e secondo la stessa logica, sulla pre-comprensione del numero e sulla precomprensione dell’operazione sul e col numero.

La totalità direttamente operatoria della matematica insegnata attualmente, si radica in ultima analisi sulla nozione di "prodotto cartesiano" AxA, ultimo referente formale di un’intuizione che non può che essere irriducibilmente binaria dell'operazione, in generale. Qualunque operazione di per se stessa non può infatti che avere la forma a*b=c.

Ora la traduzione didattica di quest’ intuizione fondamentale al livello dell’insegnamento delle operazioni elementari dell’aritmetica (le "quattro" operazioni) – e cioè all’ingresso stesso della mente infantile nel mondo dell’evidenza matematica 1+1=2 – è che l’interna duplicità logica delle due occorrenze dello stesso simbolo 1 significa la presenza davanti all’operatore di due=2=1+1 entità distinte, attuali e reciprocamente esterne, che l'operatore si occupa di assemblare, disassemblare etc. ottenendo un certo risultato finale.

Data questa precomprensione fondamentale della binarietà intrinseca di qualunque fenomeno operatorio, anche la scrittura aⁿ è interpretata come una operazione su due cose (Dinge), ciò che rende infine incomprensibili le scritture 0ⁿ, n⁰, n¹.

Didatticamente, occorre allora introdurre dapprima la nozione di numero come UNITARIO PROCESSO di CRESCITA, e l’ operazione di elevazione a potenza come operazione su [=fonemeno aritmetico concernente] UN SOLO fattore, che in sé porti – nella logica di come viene insegnata - la nozione dedekindiana di Ab-bildung (Applicazione rappresentazionale) di Ähnligkeit (Somiglianza), e di Abblidung eines Systems in sich selbst (Auto-applicazione rappresentazionale di un sistema in se stesso)… perché solo con la restituzione della duplicità cosale 1+1 alla duplicità puramente rappresentazionale che il singolo numero come tale intrattiene con se stesso (in quanto numerante/numerato) si può procedere derivativamente alla comprensione di cosa sia un prodotto tra due numeri, e cosa ne sia la somma.

Quale sarà lo strumento immaginativo didatticamente adeguato a rappresentare UN SOLO NUMERO che cresce in se stesso, alternativo all’ammassare due o più cose già esistenti l’una sull’altra?

Al posto di questa pre-comprensione di base (Mariscotti) - perfettamente comprensibile per qualunque bambino, di qualunque età:

"Due cumuli cumulati danno un cumulo più grande"

...utilizzeremo questa pre-comprensione di base - anch'essa perfettamente comprensibile per qualunque bambino, di qualunque età:

"Applicarsi con costanza aumenta la propria POTENZA"

Il bambino che apprende vede in questo caso UNA SOLA IDENTITÀ LOGICA crescere su se stessa, attraverso la sola applicazione di sè sul proprio "sistema" a se stesso riferito (sich-selbst ab-gebildet).

Né l'atleta nel suo tutto, né la singola parte che lo costituisce, accumulano in questi casi cose su cose: il fenomeno è quello dell'unitario processo di una sola applicazione di forza erogata ripetuta nel tempo, che genera step by step la crescita[trasformazione] su se stessa di una certa configurazione fenomenica. Il muscolo allenatissimo è infatti nella sua apparenza certamente dissimile dal muscolo d'inizio, così come un pulcino al momento dell'uscita dall'uovo è diverso dal tuorlo/albume presenti all'inizio, e così come il simbolo 3 è diverso dai simboli 0,1 e 2 e il numero 3 è del diverso dai numeri 0,1 e 2 in quanto portatore di proprietà che in essi sono del tutto assenti. Nel caso dell'uovo, la trasformazione avviene in completa assenza di accumuli o aggiunte di altra materia bianca o arancione, e allo stesso modo l'atleta che si [= sich selbst] potenzia attraverso la sola applicazione [=Ab-bildung] non sta ingerendo materia muscolare (semmai continua a respirare... cosa che però fa anche se non si allena).

Non ci sarà dunque bisogno, sulla base di queste pre-comprensioni elementari, di pensare a 2 come all'accumularsi di 1 & 1, perché "2" è senz'altro comprensibile come un fenomeno di [auto]potenziameto (aumento della porpria potenza) così come mostra il sistema di numerazione posizionale al cui interno, qualunque sia la base prescelta, assistiamo a un progressivo aumento, non di taglia ma di potenza combinatoria, via via che si succedono numericamente gli esponenti della stessa base: "unità" non significa infatti 10¹, ma nove possibili configurazioni simbolico/numeriche; "centinaia" non significa 10², ma novantanove possibili configurazioni simbolico/numeriche etc.

La stessità logica del processo mostra così di essere la BASE, che è uguale per tutti i numeri al grado 0, e cioè prima del primo step di applicazione (esponente 1), che come tale si limita dunque a rendere visibile la base stessa. Nella successione 2,4,8,16… il "2" non è la base, perché la base è la fonte logica dell’identità dell’intera progressione, e cioè il 2 generatore della progressione 2⁰, 2¹, 2², 2³, 2⁴). In questo caso, l'immagine della ghianda e della quercia sarà perfettamente adeguata: al livello del seme 0, tutti le parti 1,2,3... dell'albero dei numeri - radici, tronco, rami, foglie frutti, a qualunque livello del loro sviluppo - sono ancora inespresse, non manifestate, non rappresentate [=nicht aus-gebildet]..., ma sono in potenza tutte presenti.

In che modo si renderanno dunque accessibili il PRODOTTO e la SOMMA? Così:

Acqua e bimbo GIUSTAPPOSTI si SOMMANO per PRODURRE nutrimento

Invece di far capire in quinta elementare che ogni numero intero è per ciò stesso una frazione (programma di classe quarta e quinta: "Scritture diverse dello stesso numero: frazione, frazione decimale, numero decimale ) facciamo innanzitutto capire che ogni numero è per ciò stesso una potenza.

Si mostra in questo modo che il prodotto di due numeri n x m è condizionato alla presenza almeno al primo grado della potenza n¹ e m¹ di ognuno di essi (altrimenti si ha semplicemente n x 1 o m x 1 o 1 x 1), che è come dire che per bere bisogna 1) essere in vita=possedere una potenza interna; 2) essere nati= possedere una configurazione visibile attuale).

Questo renderà comprensibile la moltiplicazione nei termini del primo teorema dell'aritmetica: ogni numero è un composto moltiplicativo di numeri primi - così come ogni nota è un composto di armonici fondamentali - e la divisione non come tagliare o segare cose materiate, ma come riconduzione ad elementi primi, ognuno dotato di un irriducibile potere di identificazione logica del composto cui partecipa (numero primo = armonico logico). La scomposizione in numeri primi permette infatti l'ottenimento di un comun divisore/multiplo alla sola condizione che ogni elemento primo di base venga lasciato logicamente intatto : 32 [2⁵] può infatti venire venire trasformato in 8 [2³](o viceversa) - col trasformare l'esponente 5 nell'esponente 3 - se stiamo cercando un divisore/multiplo comune tra 96 [=2⁵x 3], e 24 [=2³ x 3]. Al contrario, se modifichiamo l'identità logica della base 2, smarriamo ogni orientamento nella ricerca di ciò che accomuna - nella divisione o nella moltiplicazione, e dunque nella loro identità razionale - i due nuleri 96 e 24.

Questo mostra che l'esponente non è un numero logicamente autonomo, perché esso non indica che il grado di presenza logica di una certa identità numerica - la base - , e il numero-esponente è un numero [un armonico logico] puramente interno al numero-base.

Una volta capito che il Prodotto presuppone la Potenza, si mostra che la Somma presuppone il Prodotto: solo a questo punto mostrando (come terzostep, dopo l'introduzione di n e di n¹, che n/1 non è che un altro modo ("razionale=logico") di esprimere il naturale n, e dunque il numero-potenza n¹. Infatti, ogni numero-potenza è già di per sé un prodotto (composizione di primi) e dunque una potenziale frazione, con denominatore 1, e solo perché due "interi" n e m sono in realtà n¹/1 e m¹/1 - e cioè - ... allora si possono sommare: perché se il de-nominatore non fosse lo stesso 1 non potremmo sommarli, così come lo stesso bimbo che beve non può respirare acqua, perché anche se si giustappone acqua e alveolo polmonare non si produce alcuna sintesi, né di somma né di prodotto - e secondo lo stesso principio il pesce che respira acqua non può nutrirsi di aria.

Tutto il resto del'aritmetica discende con naturalezza da questa base, e anche tutto il resto della matematica, perché su questi fondamenti si intende con chiarezza anche l'arrivo dell'"incommensurabile" .

---

^[1A] Su tutto questo, cfr. la pagina di presentazione generale dell'Offerta Formativa di Eironeia, e le considerazioni epistemologiche generali sui paralogismi che affliggono l'immaginario scientifico attuale.Quanto a Frege, il suo scandalo era proprio questo stesso scandalo: "Non è vergognoso [beschämend] per la scienza, che essa debba essere così confusa riguardo al suo oggetto più più originario, e in apparenza così semplice? Non c'è da aspettarsi che si sappia dire cosa è il Numero. [...] Il presente scritto mostrerà che anche un passaggio in apparenza così banale come quello da n a n+1 si fonda sulle generali leggi logiche [den allgemeinen logischen Gesetzen] e non ha bisogno di particolari leggi del pensiero aggregativo [besondrer Gesetze des aggregativen Denkens. Certo si può fare meccanicamente uso dei numeri, così come si può parlare a pappagallo [papageimässig], ma difficilmente si potrebbe chiamarlo "pensiero". È in effetti possibile, dopo che la lingua dei segni matematici [die mathematische Zeichensprache] sia stata costruita attraverso un autentico pensiero[durch wirkliches Denken] che essa, per così dire, pensi per noi. Ma questo non prova che i numeri sono costruiti in un qualche particolare modo meccanico, come i granelli di sabbia da grani di quarzo.[Gottlob Frege, Die Grundlagen der Arithmetik Breslau 1884, mia trad.]