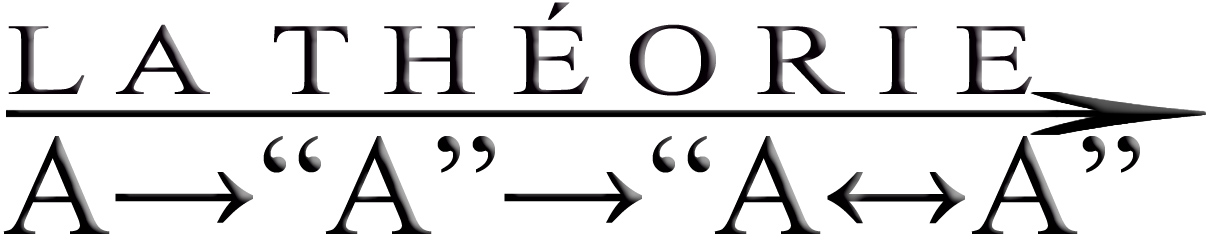

Ce travail – Le fait génétique… – a comme but la fondation expérimentale d’une assertion d’existence. Cette assertion, ma THESE, est (p.15): un mental humain existe comme réalité substantielle, qui déploie sa force évolutive et créatrice tout le long de notre vie, et qui est aussi irréductible à notre cerveau que la «masse» m est irréductible aux corps qui en manifestent la présence au travers de leurs façons de bouger.
En revanche, le PHENOMENE ciblé pour mener à bien ma démonstration est : un homme apprend à lire, et à la suite de cet apprentissage l’évidence mathématique fait son apparition devant sa conscience.
En synthèse, ce que je me propose de montrer est que ce double événement ne peut s’expliquer que comme la manifestation d’une même force bien réelle et physique: notre force mentale, ou la « puissance dynamique » de notre mental.
La formule symbolique que j’ai choisie pour exprimer l’unité de ce phénomène est la suivante:

…que je lis comme «A perçu» produit «A lu» produit la saisie de la vérité mathématique évidente « A double implique A ». Dans cette formule, le premier « A » signifie la perception de l’objet graphique sur lequel notre voix – qui affirme «ceci est A» – se concentre quand nous devons apprendre à le lire ; le deuxième « “A” » signifie l’événement final de la lecture de ce même A comme une lettre ; troisièmement, l’expression « “A<-->A” » signifie le jugement explicite « A est A », consciemment prononcé comme une vérité logique évidente, lorsque le sujet lit cette formule comme une «tautologie».
En un mot, avec une analogie newtonienne j’affirme que de même que la force de gravitation se déploie identique à elle-même au travers de la totalité des galaxies, pour pénétrer sans solution de continuité jusqu’au coulé de l’encre sur ma feuille au travers de mon stylo, de même une seule force psychique est responsable tant de la chute de la lettre A dans ma perception, que de l’éclat d’évidence qui m’impose d’affirmer que « A<--->A » est une vérité universelle.
Or cette manière, si synthétique, de présenter le but de mon travail, ainsi que la trajectoire choisie pour le mener à bien sont enfin l’expression distillée d’un souci d’ordre irréductiblement éducatif et pédagogique. Je m’explique
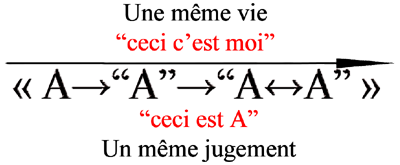
Si nous considérons les quatre « A » de ma formule, nous voyons qu’ils expriment en même temps : (1) l’unité/identité biographique de la vie d’un même homme, jalonnée en deux étapes ; (2) l’unité/identité d’un seul et même jugement concernant quatre occurrences d’un même objet (A) à la fois physique, graphique, symbolique, logique.
Comme le même homme doit bien avoir parcouru chacune des étapes nécessaires à la finale apparition de la vérité mathématique devant sa conscience (apprendre à parler, apprendre à lire, apprendre à calculer…), je suggère qu’une une première équivalence quantitative peut être établie: dans la mesure où ces quatre « A » sont le même « A », dans cette même mesure l’homme qui, grâce à l’application persévérante d’une seule et même force d’apprentissage, passe de l’un à l’autre… est un même homme.
Cela dit, pourquoi, ai-je ressenti l’exigence d’établir une telle correspondance entre l’évolution biographique d’un même homme et l’évolution du sens d’un même objet graphique/symbolique ? C’est ici que ma propre biographie peut fournir un éclaircissement. Je suis né en 1967 : ce qui signifie que j’ai pris de plein fouet la vague des « mathématiques modernes ». De plein fouet signifie que pour moi les mots de ces textes étaient la vérité définitive, et ces textes parlent comme cela (p.38):
(14)« Définition. - On appelle puissance d’un nombre relatif le produit de plusieurs facteurs, tous égaux à ce nombre : an = a . a · a …· a (n fois) [...]. Sur la base de cette définition de puissance, l’écriture a1 serait DEPOURVUE DE SENS; on pose alors par convention que cette base est égale à a, à savoir a1 = a. – […] Supposons maintenant a0, et considérons l’identité an:an= 1 (le quotient d’un nombre divisé par lui même est égal à l’unité); si dans l’égalité qui exprime la propriété citée nous posons m=n, nous obtenons an:an= an-n=a0 qui est un écriture formellement dépourvue de sens. Puisque nous avons constaté que an:an= 1, il est spontané de poser la convention a0. » [Chiellini 1980: 85-88. Ma trad. L’italique est de moi.]on pose alors par convention que cette base est égale à a, à savoir a1 = a.
«Sur la base de notre définition de la puissance dans les termes d’une suite de multiplications - affirme l'auteur - les expressions « a0» et « a1 » sont dépourvues de sens – car une multiplication avec un seul ou zéro facteurs n’a aucun sens – : il est donc spontané de poser par convention qu’elles sont néanmoins valables ».
Ces mots décrivent parfaitement ce qui a provoqué dans mon esprit le « tournant pédagogique» qui a inspiré toutes mes recherches le long de dernières 12 années. L’auteur nous dit deux choses : a) qu’une certaine évidence mathématique rayonnant sa vérité ici et maintenant devant nous est néanmoins « totalement dépourvue de sens »; b) que dans un cas pareil notre « réaction spontanée » est de « poser par convention qu'elle est néanmoins valide
La première affirmation (le manque de sens d’une opération sur aucun ou un seul élément) est la conséquence immédiate de la définition de l’opération mathématique dans les termes que Bourbaki utilise dans ce passage (p.44)
20 I. « Faire de l'Algèbre, c'est essentiellement calculer, c'est-à-dire effectuer, sur des éléments d'un ensemble, des « opérations algébriques », dont l'exemple le plus connu est fourni par les « quatre règles » de l'arithmétique élémentaire. […] II. Dépouillée de tout caractère spécifique, la notion commune sous-jacente aux opérations algébriques usuelles est fort simple : effectuer une opération algébrique sur deux éléments a, b d'un même ensemble E, c'est faire correspondre au couple (a, b) un troisième élément bien déterminé c de l'ensemble E.» [Bourbaki 1970 : 1.]
La deuxième affirmation de Chiellini, en revanche, incarne l’orientation générale d’une politique éducative : elle nous dit non pas ce qui est effectivement spontané dans un cas pareil – lors de la première rencontre d'un enfant avec un flagrant non-sens mathématique – mais ce qui doit le devenir étant donné les finalités fondamentales de l’enseignement des mathématiques dans notre civilisation.
En fait, si nous observons la Fig.3 (p.37) dans mon texte…

…nous pouvons ré-vivre en directe le moment même où notre mouvance spontanée ne décide certes pas de « poser par convention » quelque chose de totalement incompréhensible, mais bien au contraire se demande ce que l’âme Socrate se demande dans le célèbre livre VIIe de la République autour des flagrants non-sens que seules les mathématiques sont en état de produire avec un tel degré de violence : ti pote semainei… qu’est-ce qu’il est en train de se passer ? La limite qui sépare les passages I-II des passages III etc. dans la Fig.3 identifie donc très clairement le moment où la biographie d’un homme a l’occasion de prendre un tournant tout à fait imprévu et inoubliable, essentiellement à cause du fait qu’un un certain enchainement graphico/symbolique a pris à son tour un tournant tout à fait imprévu, qui demande une profonde et définitive résignification de ce que l’on est en train de faire et savoir, lorsqu’on « fait de l’algèbre » comme Bourbaki s’exprime : et cela, soit que l’on décide pour la « convention », soit que l’on décide pour la voie socratique et cartésienne de la CONTEMPLATION.
Mon idée est en synthèse que ce moment si crucial est insécablement d’ordre mathématique et éthico/pédagogique : le mathématicien créatif n’est à mon sens en fait nul autre que l’élève/enseignant qui refuse de se résigner au non-sens soudainement apparu sur la surface de ce que jusqu’ici était la pierre de comparaison de tout ce qui est vrai, évident, fondé, indubitable… et qui considère comme « spontané » ce sens « pure et noble de la démonstration » dont parle Dedekind dans sa célèbre lettre à Lipchitz du 1876 (p.320, note 8)
« Mais n'est-il pas proprement révoltant que l'enseignement des mathématiques à l'école passe pour un moyen éminemment efficace pour former l'entendement, alors qu'aucune autre discipline (comme par ex. la grammaire) ne tolérerait un seul instant des infractions si grossières à la logique ? Si l'on ne veut pas procéder scientifiquement, ou si on ne peut le faire faute de temps, que l'on soit au moins honnête et qu'on l'avoue aussi franchement aux élèves déjà si enclins à croire un théorème sur parole du maître ; cela vaudrait mieux que d'étouffer ce sens pur et noble de la vraie démonstration en usant des pseudo-démonstrations. […] Je soutiens en même temps que la plus grande partie (en fait la quasi intégralité) de ces théorèmes de l'arithmétique n'ont pas été démontrés jusqu'ici» [À Rudolph Lipschitz. Dedekind 1876 : 41]
Ce que je viens d’exposer explique donc l’impulsion primordiale et toujours agissante qui m’a conduit à la suite développementale, biographique et sémantique de mes quatre A. Les mathématiques telles que je le prends en considération dans cette thèse sont l’horizon toujours éclairé d’une incessante activité de résignification, et étant donné la force des évidences qui les constituent, tout choix interprétatif qui se fait à l’intérieur de cet horizon a un poids éthico/pédagogique que rien ne peut égaler au niveau de nos apprentissages de base.
En somme, à l’opposé de ce que Bourbaki affirme, «calculer» est pour moi essentiellement prendre des décisions responsables autour du sens des symboles qui s’entresuivent devant nos yeux et dont la voix – qui est la nôtre – retentit dans nos oreilles. Un « mental humain » existe signifie donc, enfin, un homme existe, qui a la force d’attribuer un sens nouveau à ses pratiques de vie et de connaissance, là où tout sens paraîtrait au contraire avoir fait définitivement naufrage.
Tout ce que j’ai dit jusqu’ici rend bien visible l’objet mathématique que j’ai visé dès le début. Il s’agit à proprement parler non pas d’un objet mais d’un phénomène, que je fais agir comme la voix la plus essentielle de l’activité mathématique. Aussi paradoxal qu’il soit, ce phénomène est celui de la disparition du sens de nos symboles, qui nous laisse en présence de leur pure et simple apparence graphique.
J’ai cherché dans la phénoménologie de la dissolution du sens de nos symboles cela même que les textes cités refusent : non pas un épisode à refouler au nom de la « convention » mais bien au contraire l’expression de la nature essentiellement bipolaire du dynamisme propre à la transformation mathématique.
Vous avez un exemple éminent de cette perspective dynamique, phénoménologique et développementale au §3.2 (p.37-38), où je montre que du point de vue à la fois opératoire et subjectif, que la ratio de la suite grandeurs--> nombres naturels-->rationnels-relatifs-->réels est celle de la transformation, qui se répète à chaque passage, d’une impossibilité absolue en une nécessité aussi absolue que cette même impossibilité de départ.
Exemple : l’opération 3 : 2 est impossible, car 3 n’est pas pair – à savoir 3diff.2n, et toutefois l’opération 3/2×2=3 est une évidence. Soit donc 3/2=a. Nous dirons alors que 2a=3… ce qui est impossible, à moins que nous ne décidions que a est un nouveau nombre, c'est-à-dire un nouveau sens du même mot «nombre». Nous avons ainsi créé une évidence en transformant une impossibilité en une nécessité.
Cette dynamique de «trans-modalisation» est pour moi le fil rouge qui conduit, sans solution de continuité, de la première apparition des nombres pairs/impaires au sein des « grandeurs » (en principe toujours dichotomisables, donc « paires ») jusqu’à l’apparition des nombres réels au cœur du corps de rationnels.

De même que 3/2 du point de vue des naturels, v2 est un nombre impossible du point de vue des rationnels, et toutefois il devient par là même, justement au travers d’une telle déclaration d’impossibilité, la graine d’une nouvelle dimension de l’évidence nécessaire. Mon idée a donc été la suivante : la vie la plus intime et vraie de l'activité mathématique est exprimée essentiellement par cette PULSATION TRANSMODALE DU SENS. [cf.aussi ma notion didactico/pédagogicue de "choc réveillant"]
En dévoilant donc dès maintenant le résultat final de mon parcours démonstratif, ce que j’ai fait est de suivre la plus élémentaire des exigences de continuité, en reculant mon attention expérimentale jusqu’à avant le moment où la première dichotomie grandeurs/nombres fait son apparition devant notre conscience, et cela, bien entendu, sans jamais quitter notre phénomène de référence, qui est la présence d’une évidence mathématique écrite devant notre attention). Ce que j’ai obtenu apparaît dans la Fig.83' de mon travail (p.253).

Dans cette image, le périmètre d’un seul et même « trait de plume » enferme le monde de l’écriture mathématique alpha/numérique. Cela signifie qu’une préalable dichotomie lettres/grandeurs-nombres doit articuler le monde de la lecture/écriture, avant que la dichotomie entre grandeurs/nombres (Diapo 11) ne puisse à son tour faire son apparition. De sa part, ce même « trait de plume » – la grammé d’Euclide – capable de véhiculer des évidences mathématiques une fois que nous avons appris à lire, ne peut acquérir cette vertu purement subjective que grâce à l’intervention intentionnelle de notre voix sur des simples graphèmes perçus. (cf.§11 «L’arabesque de Galilée» - §11.1 La fréquence de la voix et la naissance de la grammé, pp.217-228).
Ma perspective est donc éminemment dynamique et développementale en ce qu’elle regarde aux mathématiques comme à un phénomène irréductiblement bipolaire et mouvant, qui se déploie à tous les niveaux suivant la directrice développementale de notre apprentissage. Quant à l’assertion qui apparaît dans la Fig.83', elle a une « saveur » manifestement trascendentale, qui s’explique désormais très bien sur la base de ma « dynamique trans-modale de pulsation du sens ». Selon Kant (citation <15> p.40):
« Montrer comment un certain concept est un principe qui explique la possibilité d'autres connaissances synthétiques a priori, voilà ce que j'appelle en faire une exposition transcendantale» [Kant,1787a: 145,73.].
Si un mouvement transcendantal de notre pensée signifie qu’elle se rapporte – en la [re]mettant en question – à la possibilité d’une certaine vérité apriori (comme a1=a), alors la perplexité devant une opération mathématique à la fois évidente et incompréhensible est une mouvance transcendantale animée par l’intention inébranlable qu’un sens doit bien demeurer intact sur le fond d’une vérité si incompréhensible.
Ma démarche vise donc à bien isoler expérimentalement un champ d’attention transcendantal à l’intérieur duquel notre phénomène de pulsation polaire du sens prend corps, et ce champ nous confronte à deux éléments résiduels frontalement disposés : d’une part nos mots – qui doivent bien garder un sens lorsque nos symboles nous ont abandonnés – et de l’autre nos graphèmes, qui se chargent néanmoins de rester la présence bien signifiante d’une énigme, jusqu’au moment où ce non-sens se transformera en un sens nouveau.
La dimension externeoù cette frontalité essentiellement génétique, évolutive et développementale entre mots et graphèmes prend corps est le champ de l’apprentissage scolaire, tandis que sa dimension interne est le mental humain, qui se définit en conséquence comme une force herméneutique incessamment rayonnant de notre présence, et qui doit être bien présente et agissante tout le long d’une « oscillation complète » du sens : évidence, impossibilité, nouvelle évidence.
Tout ce que je viens d’exposer explique bien la structure de la deuxième et de la troisième partie de mon travail [Réorienter le développement, et Redonner une voix à l’homme]. Du point de vue méthodologique, je poursuis la fondation d’une dynamique évolutive du sens à l’intérieur de la biographie d’un homme. Cela me situe sur la directrice qui très explicitement lie l’œuvre de Jean Piaget à celle de Galilée.
«Toute connaissance, qu’elle soit d’ordre scientifique ou relève du simple sens commun, suppose un système, explicite ou implicite, de principes de conservation. Dans le domaine des sciences expérimentales, il n’est pas besoin de rappeler comment l’introduction de la conservation du mouvement rectiligne et uniforme (principe d’inertie) a rendu possible le développement de la physique moderne, ni comment le postulat de la conservation du poids a permis à Lavoisier d’opposer une chimie rationnelle à l’alchimie qualitative. Il est évident que la pensée arithmétique n’échappe point à une telle règle. Un ensemble ou une collection ne sont concevables que si leur valeur totale demeure inchangée quels que soient les changements introduits dans les rapports des éléments […] Un nombre n’est également intelligible que dans la mesure où il demeure identique à lui-même quelle que soit la disposition des unités dont il est composé : c’est ce qu’on a appelé l’« invariance » du nombre. » [Piaget 1941 : 16-17]
Toute connaissance – écrit Piaget dans ce passage extrait de La genèse du nombre chez l’enfant – suppose un système, explicite ou implicite, de principes de conservation. Cela a été le cas de la physique de Galilée et de la chimie de Lavoisier. «La pensée arithmétique n’échappe point à une telle règle : car un nombre n’est également intelligible que dans la mesure où il demeure identique à lui-même quelle que soit la disposition des unités dont il est composé ». Jean Piaget se propose donc de répéter, au niveau des transformations mentales qui jalonnent notre développement, la même opération de mathématisation que Galilée a réalisée dans le domaine des transformations physiques. Mon souci majeur est d’autre part celui de montrer (cf.§10.1(1)(2) p. 174-182, particulièrement 174-176 et 181) que, réciproquement la perspective de Galilée est à son tour rigoureusement génétique, en ce que sa dynamique mathématisée fonde une vision cosmogonique des phénomènes.
Piaget est bien le Galilée de la psychologie,en ce qu’il se propose de mathématiser nos cinématiques mentales en les ramenant à leurs structures dynamiques fondamentales, qui sont exhaustivement modélisables, selon lui, au travers de la structure algébrique du groupe.
Tout au long du §6 je m’occupe de montrer l’isomorphisme très rigoureux qui lie les démarches galiléennes visant à établir et mathématiser un principe de conservation en physique, et les démarches piagétiennes, visant à mathématiser la source intérieure et purement subjective de cette même exigence conservatrice. (Fig.33 p.95)

Cette figure (la Fig.33 p.95) montre ce que j’ai obtenu en empruntant ce chemin : l’évidence d’un phénomène développemental de décalage entre les difficultés perceptives que les enfants en âge préscolaire interrogés par Piaget ont à « conserver le nombre » et la « quantité continue » lorsque l’apparence perceptive d’un certain récipient (contenant des jetons ou de la boisson) passe du « couché » au « dressé », et les difficultés projectives endurées par les interlocuteurs de Salviati dans le Dialogue sur les grands systèmes de Galilée, lorsqu’il s’agit de saisir la conservation d’une même constante physique. Ici (les deux figures sur la droite) un même « élan » se conserve malgré la grande différence d’inclinaison entre les deux plans inclinés, et les pauvres Simplicio et Sagredo doivent endurer des sérieuses difficultés pour s’en convaincre. J’en conclus que Piaget a bien raison lorsqu’il défend la « continuité fonctionnelle » de nos mécanismes mentaux tout le long de notre développement : de notre enfance jusqu’aux plus hauts sommets de la science une même « dynamique expérimentale » intervient sur notre monde, interne et externe, pour lui donner une cohérence et une cohésion toujours plus riche et profonde.
Or, sur cela j’oppose très vivement les résultats de la recherche piagétienne aux critiques que lui a adressées la psychologie évolutive (notamment américaine) pendant les dernier 40 ans (§6.2, pp.75-83). En fait, si Piaget a compris qu’une irréductible distance évolutive sépare le mental ordinaire (et donc enfantin) du nombre pleinement mathématique, ces chercheurs ont en revanche montré la présence indéniable d’un « nombre » chez les nourrissons et même chez les animaux. Il s’agit d’un résultat certes précieux, mais cela n’empêche que la démarche de ces psychologues n’est pas en mesure d’établir une vraie et pleine continuité entre la « numérosité » saisie par l’enfant préscolaire et l’évidence mathématique appréhendée par ce même enfant une fois qu’il a appris à lire. En synthèse : un vide sépare le nombre indéniablement perçu par le petits et le nombre lu et calculé par leurs frères aînés, et de ce vide ni Piaget ni ses adversaire ne savent nous rendre compte. C’est bien sur ce gouffre que je me suis proposé de jeter un pont, et je l’ai fait en renouant les processus mentaux des petits non pas à ceux de notre pensée adulte ordinaire, mais bien au contraire aux procédés mis en œuvre par les grands mathématiciens qui ont fait la gloire de notre science.
Cette hypothèse de travail est bien exprimée par cette image…
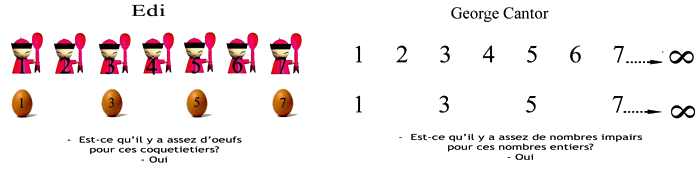
… qui montre un indéniable isomorphisme entre la « faiblesse » du mental enfantin, incapable de faire de la correspondance un-à-un un critère de détermination de la quantité d’éléments d’un ensemble donné – car l’enfant reste victime de l’équivalence perceptive des deux ensembles comparés – et la force mentale du grand mathématicien, qui transforme cette même erreur en une extraordinaire source de vérité. Ma conclusion a été que le grand mathématicien est un enfant préscolaire « décalé ». C’est ici que mon modèle développemental explicitement abandonne l’orthodoxie piagétienne, pour procéder vers une intuition à mon sens plus cohérente et complète de nos transformations mentales, tout le long de notre vie. (Fig. 43 p.120)

Ce qu’il faut retenir de cette image (Fig.43 p.120) est l’identité fondamentale que j’établis entre les dynamiques profondes et primordiales de notre esprit enfantin (magique et syncrétique), et la force créatrice qui propulse les mouvances mentales du grand mathématicien. Au milieu, nous observons le monde des évidences ordinaires, aussi incapables de comprendre le monde magique de l’enfant que d’atteindre les visions « bewildering and exhotic » (Gelman and Gallistel:cit.<79>p.81) des grands mathématiciens.
Quant à la notion logiciste d’ « application » a=f(a), il s’agit de ma riposte à l’option bourbakiste qui rend nécessaires au moins deux éléments déjà existants pour qu’une opération algébrique ait lieu, et qui conduit à la déclaration de non-sens de a1=a. Mon idée est, en un mot, est que non pas la structure déjà structurée du groupe (avec sa réversibilité caractéristique) mais seulement celle, irréversiblement structurante de l’« Abbildung » à la racine dynamique de toute cinématique groupale, peut rendre compte de l’unité globale de notre évolution mentale, c'est-à-dire de l’entière biographie d’un seul et même sujet opératoire. Le sens de cette re-modélisation des mécanismes fondamentaux de notre pensée dans les termes d’un fond dynamique pré-groupal et d’une surface cinématique groupale déjà achevée est bien saisissable si nous revenons à cette « pulsation trans-modale du sens » qui définit ma perspective dynamique, et que je vois agir tout le long de notre apprentissage mathématique. En bref : si, le moment venu, le groupe des nombres rationnels fait son apparition au cœur du nombre naturel, cette structure est bien impossible du point de vu de ce même monde de provenance, qui est pourtant bien nécessaire pour que cette apparition se produise. Il faut donc tout simplement refouler l’instant où le mathématicien a eu le courage de forcer le 3 à se diviser en deux parties égales, en créant de la sorte une entité impossible (un nombre 2n impair) et pourtant évidente, pour ne pas reconnaitre qu’à ce premier passage des naturels aux rationnels ne correspond pas une opération inverse. Autrement dit : la mise-en-action d’un groupe n’est pas un groupe, car elle a un sens, une orientation interne par rapport à laquelle on ne revient pas en arrière.
Dans le §8 je m’occupe de fonder cette affirmation au niveau directement mathématique : je discute la notion de groupe tant du point de vue historique que directement formel, et je me trouve confirmé en mon hypothèse. Il s’agit d’une conclusion, on le voit bien, tout à fait fondamentale, car elle me permet de souder une perspective directement mathématique à ce que j’ai dit à propos du champ transcendantal (scolaire et mental) où se déroule la totalité de notre apprentissage. Notre vie entière en résulte caractérisée par une inépuisable activité de [ré]orientation de nos cadres cognitifs et existentiels, qui acquirent de la sorte un sens toujours nouveau et tout à fait irréductible à leur monde de provenance.
Toute la troisième et dernière partie de mon travail – Redonner une voix à l’homme – vise à analyser cette hypothèse, et à montrer que cette activité d’incessante réorientation n’est pas, à son origine, d’ordre spatial et en ce sens « matériel », mais irréductiblement herméneutique : l’orientation dans l’espace est en réalité le phénomène de surface d’une activité de résignification du sens de nos cadres de vie, c'est-à-dire de notre histoire.
Ce que je fais dans cette partie finale est donc de rendre le sens à lui-même, en en faisant la matière première de notre corps: une matière bien matérielle donc – car nous sommes indéniablement de la matière – mais dont la substance ultime ne sont pas des « atomes » ou des « particules » opaques à toute signification, mais des événements et des histoires qui tissent la trame d’un tissu essentiellement narratif. Je fonde cette hypothèse à tous les niveaux de l’enquête : (1) métaphysique – en redécouvrant la notion aristotélicienne de l’être en puissance – ; (2) physique, en soumettant à une analyse très détaillée les phénomènes fondateurs de notre science : les phénomènes mécaniques du pendule, du plan incliné, du choc entre deux corps, ainsi que les phénomènes électriques de la pile et de la dynamo. Il en résulte que rien ne nous permet de dire que la matière qui nous constitue est faite de « choses spatiales » comme Einstein le dit (cf.§10.1(0) p. 172), et que les phénomènes nous obligent à reconnaitre – avec Wittgenstein – que la trame du monde est celle d’une suite d’événements, qui trouvent leur expression éminente dans le phénomène de la fréquence, c'est-à-dire du temps interne qui jalonne la vie et la voix des faits que nous sommes, et qui nous entourent.
Finalement, (3) j’explore la dimension logico/mathématique de cette affirmation, en me proposant de montrer que l’unité interne du phénomène de la démonstration mathématique est d’ordre univoquement événementiel et narratif, car l’éclat d’une évidence mathématique n’est enfin rien d’autre que le reflet de la force expressive (la voix) que notre être projette sur le monde, en prétendant que « tout ce qui se passe » puisse avoir un sens.
Dans le §10-§11 j’ai en somme l’ambition de démontrer que la voix humaine – l’intention de parler – est à la racine de sa propre fréquence, de son isochronisme et de son individualité absolue : la fréquence de notre voix est le fruit de notre inébranlable intention de nous exprimer, et pas l’inverse. Grâce à ce renversement, notre voix (sa sonorité perceptible) s’avère être le fruit d’une « attraction fréquentielle » exercée par notre être corporel – désireux de s’auto-manifester – sur l’un de ses membres (nos cordes vocales). Ce processus d’autre part se répète identique dans le cas de l’apprentissage à lire/écrire, car c’est bien notre voix qui engendre la transformation d’une ligne d’encre en un enchaînement d’expressions signifiantes, immédiatement transparentes au sens que nous percevons à leur intérieur.
Si j’ai raison, alors une même force, la force de donner un sens à notre vie personnelle et incarnée engendre premièrement la formation de notre voix, ensuite celle de notre écriture, pour finalement faire éclater, au sein de cette même écriture, la lumière de l’évidence mathématique, qui n’est autre que le retentissement final de ce postulat fondateur : ma vie, le monde que j’habite et qui m’habite doit bien pouvoir avoir un sens.
La thèse rejoint ainsi sa conclusion.