La genèse des mathématiques et la puissance dynamique du mental humain



IMAGES

Première ¨Partie - Réincarner les mathématiques

Figure 1 - Quatre perspectives sur la Tour Montparnasse.Dans le quadrant B nous sommes en bas et nous regardons vers le ciel. Dans le quadrant D nous sommes sur le toit et nous regardons vers la terre.

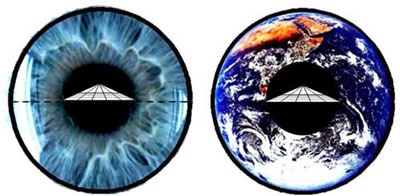
Figure 2ab - (a) À gauche, une perspective cavalière créée par notre œil ; (b) à droite, les directrices gravitationnelles de la terre, « vues » du point de vue de la terre même.

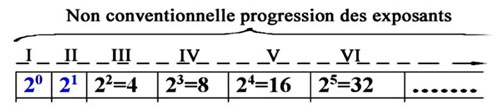
Figure 3 - Les choses toutefois changent radicalement lorsque du cœur de cette même évidence surgit un jour la séquence « banale » 2²-->2¹-->2⁰; dans ce cas, cette énigme est le véhicule immédiat de sa mémoire interne. Pendant longtemps – un temps dont à ce stade l’élève garde la mémoire – 2élévé2 a été expliqué avec 2+2, tandis que maintenant … tout devient obscur. À la différence du stade précédent (le passage ne pas savoir lire 1, 2, 3 --> percevoir 1, 2, 3) il reste présent et en état d’éveil lorsque les échelons III, IV, V,VI… de la suite en Fig. 3, s’enrichissent des échelons absolument incompréhensibles I et II. En même temps il comprend parfaitement (III, IV, V, VI…) et il ne comprend absolument rien (I : une multiplication avec 0 facteurs ; II : une multiplication avec un seul facteur)

Figure 4 [1] Nous disons : « puisqu’elle se déplace en (I), la sphère A pousse la sphère B en (II) et en conséquence de cette poussée le mouvement dont la boule A était douée passe à la boule B, qui donc se déplace à son tour, en parcourant en (III) la distance ?s ». Autrement dit, nous pensons que si un corps en pousse un autre, c’est grâce à son propre mouvement, c’est-à-dire à son propre déplacement, car pour pousser il faut bouger, et ne pas se déplacer signifie ne pas bouger, puisqu’aucun mouvement local ne peut – évidemment ! – être dans un corps qui ne se déplace pas. Et pourtant, nous avons tort…

Figure 5 - [2a] Les Sphères de Newton [Fig. 5] nous montrent justement une telle chaîne de conduction du mouvement dont l’un des effets est le déplacement, mais pas le seul. Disposons les sphères A et B de l’exemple en [1] dans la suite ABCDE. Ainsi qu’en [1.II], en [2a.II] A frappe B, mais maintenant ni B ni C ni D ne se déplacent, tandis qu’en 2a.III, E se déplace de la même façon dont B se déplace en [1.III], c’est-à-dire en parcourant la distance ?s. Si donc en [1] nous affirmons que le mouvement passe de A à B grâce au contact en [1.II], cela nous oblige à dire la même chose maintenant : en [2a.II] le mouvement de A passe-et-donc-est en BCD, même si ces corps ne parcourent aucune distance. Donc, en [2a.II] les sphères BCD sont les porteurs/véhicules, sans se déplacer, du même « mouvement » que le corps E réalise en [2a.III] en se déplaçant. Autrement dit : BCD bougent sans se déplacer. De même, en [2a.III] le corps D met en mouvement le corps E sans le « pousser », à savoir D pousse E sans bouger.Le déplacement d’un corps dans l’espace n’est donc que l’un des effets qu’un mouvement peut avoir lorsqu’il passe, et donc est, dans ce même corps : et un effet présent en A ne peut pas être la cause de sa propre présence en B.

Figure 6 - [2ß] Si notre esprit se rebelle à l’idée de la parfaite immobilité d’un corps (D), pendant qu’il en pousse un autre (E), considérons le cas [Fig. 6] où en I toutes les sphères ABCD sont en mouvement vers la droite, tandis que E oscille vers la gauche. En [2ß.I] A oscille vers la droite jusqu’à l’instant [2ß.II] du choc entre la E et la D. L’effet de ce choc est que A inverse le sens de son oscillation en partant vers la gauche sans qu’aucun corps qui soit en contact avec elle ne se déplace pour la « pousser », car bien au contraire BCDE sont en train de voyager dans la direction opposée : la sphère B met donc en mouvement la sphère A vers la gauche, tout en bougeant vers la droite. Si donc un corps peut en pousser un autre tout en bougeant dans le sens contraire au sens du mouvement qu’il imprime au corps poussé, a fortiori il est concevable qu’il le « pousse » tout en étant parfaitement immobile. Conclusion : un corps en état de parfaite immobilité peut bien en pousser un autre, c'est-à-dire être en mouvement car le mouvement (dorénavant : mv) est en [passe-par] lui.

Figure 7 - Léonard de Vinci – L’Annonciation (1472/’75) - À la fin de ce double processus, vers la Terre de l'expérience, et vers le Ciel du concept, le tableau qui annonce la naissance de l’événement scientifique et de sa voix individuelle retentit enfin avec toute la puissance de son universalité cosmique.

Figure 8 - Léonard de Vinci, La Vis aérienne (1486). - Voilà donc ce qu’avec Cassirer j’appelle la quintessence de la méthode expérimentale : un sentiment tellement profond de la présence du Vrai au cœur de notre présence au monde, que l’homme qui l’éprouve ne lâche jamais la prise sur l'événement vécu. Son esprit commence alors ses allers-retours spiraliformes, qui au fur et à mesure qu’ils avancent, percent le phénomène terrestre jusqu’à le visser au ciel.

Figure 9 - Rembrandt – Le philosophe en méditation (1632) - « Mais enfin me voici insensiblement revenu où je voulais; car, puisque c'est une chose qui m'est à présent connue, qu'à proprement parler nous ne concevons les corps que par la faculté d'entendre qui est en nous et non point par l'imagination ni par les sens, et que nous ne le*s connaissons pas de ce que nous les voyons, ou que nous les touchons, mais seulement de ce que nous les concevons par la pensée, je connais évidemment qu'il n'y a rien qui me soit plus facile à connaître que mon esprit. » [Descartes 1647 : 26.]

Figure 10 - Galileo Galilei observe l’encensoir dans le Dôme de Pise Fresque de Luigi Sabatelli (Tribuna di Galileo, Florence 1841). Si nous prenons ce point de vue – ainsi que nous le faisons avec un galvanomètre qui nous signale une orientation, et avec les yeux d'un enfant qui réalisent la transformation « A --->"A"» – alors nous exécutons – ici et maintenant – cette opération de transfiguration d'un événement individuel d'où nécessairement s'engendre toute vraie (= non automatisée) mathématisation du monde.

Figure 11 - Le chimpanzé maîtrisa immédiatement cette mise en correspondance sur la base de l’apparence physique On rendit alors sa tâche plus difficile. Peut-être lui présentait-on toujours un verre à moitié plein ; mais il devait à présent choisir entre une demi-pomme ou trois quarts de pomme. Sur le plan de l’apparence visuelle, ces alternatives différaient totalement de l’échantillon initial. Pourtant, le chimpanzé choisissait systématiquement la moitié de pomme. Il fondait apparemment sa réponse sur la similarité conceptuelle entre un demi-verre et une demi-pomme. L’expérience connut le même succès avec les fractions ¼, ½ et ¾. » [Dehaene 1997 : 29.]

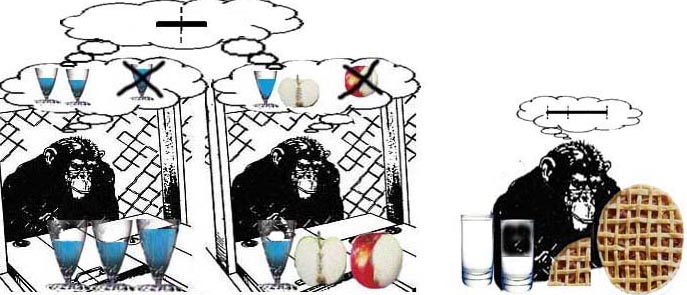
Figure 12 - [de moi] a-b) Dans sa « bulle » – son monde représentationnel – le singe est capable de saisir l’identité « fractionnaire » (le segment) d’un ensemble d’objets donné : deux demi-verres d’eau (à gauche) sont apparemment perçus comme « équivalents » à une demi-pomme ; ainsi qu’un quart de gâteau (c) est perçu comme équivalent à un quart de verre de lait.

Figure 13 - [de moi] Sans aucun doute le singe saisit la notion numérique générale « trois quarts ». Cela ne signifie pas, pourtant, que la fraction de cercle dans sa « bulle » – le signifiant intra-mental de cette même notion – soit déjà, pour le singe qui en dispose, un symbole pleinement arithmétique.

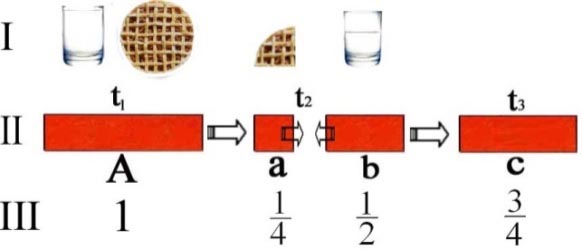
Figure 14 - La capacité d’opérer sur des quantités fractionnaires numériques n’implique aucunement la saisie de leurs propriétés irréductiblement arithmétiques, comme celle d’exiger un commun dénominateur pour que le résultat soit une évidence mathématique.

Figure 15 - ?54? « Infants in the 1+1 group were shown a single item in an empty display area. A small screen then rotated up, hiding the item from view, and the experimenter brought a second identical item into the display area, in clear view of the infant. The experimenter placed the second item out of the infant’s sight behind the screen. Thus, infants could clearly see the nature of the arithmetical operation being performed, but could not see the result of the operation. Figure 15 « Sequence of events 1+1=1 : Impossible outcome ». Réadapté de Winn 1992b. Dans les « occlusion events » étudiés par Mme Winn, le bâton en jaune est un objet réel, et pas un symbole. À cette seule condition le nourrisson peut en effet s’étonner de l’impossible outcome « I+I=I ». For both groups of infants, after the above sequence of events was concluded the screen rotated downward to reveal either one or two items in the display case. Infants' looking time to the display was then recorded. The prediction was that infants would be surprised by an apparently impossible result. Infants in the "1+1" group should look longer when the result is one than when it is two. » [Winn 1992b:749.]

Figure 16 - Si nous répétons l’expérience d’un « occlusion event » à la Winn en cachant derrière l’écran non pas un objet réel comme un bâton, mais un symbole comme « 1 », pour ensuite surprendre notre public (qui connaît l’arithmétique) avec l’impossible outcome «1+1=1 », nous n’obtiendrons pas l’étonnement souhaité.

Figure 17 - Lorsqu’il est question d’une « impossible outcome » pleinement mathématique, comme I+I=I, il n’y a pas moyen de s’en étonner, car pour s’étonner de quelque chose, il faut impérativement que ce quelque chose soit une réalité effectivement donnée.

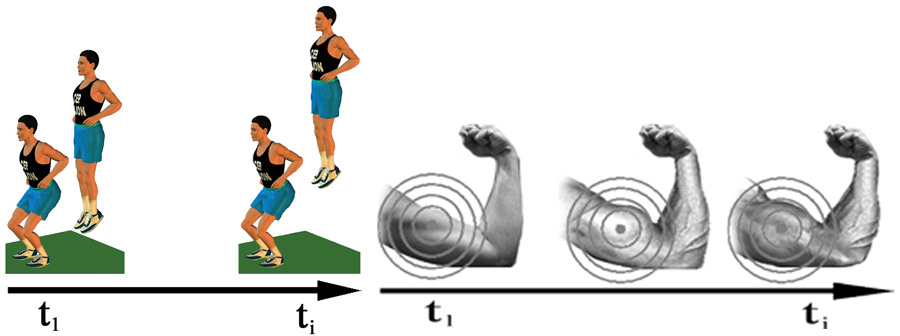
Figure 18 -Une suite quelconque d’entraînement – de notre corps en sa totalité, ou de l’une seulement de ses parties – est le « déroulement historique » d’un seul et même événement, concernant un seul et même sujet.

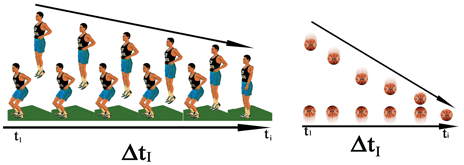
Figure 19 - Le corps vivant d’un athlète qui rebondit s’arrête nécessairement après un nombre fini de sauts, ainsi qu’il se passe dans le cas d’une balle de basket, qui n’est pas un corps vivant.

Figure 20 - L’athlète qui s’entraîne en rebondissant par terre comme sa balle de basket réalise toutefois entre-temps une progression globale de signe opposé à celle de cette dernière. Une suite de sous-vecteurs d’entraînement décroissants donne donc comme résultat global un vecteur croissant.

Deuxième ¨Partie - Réorienter le développement

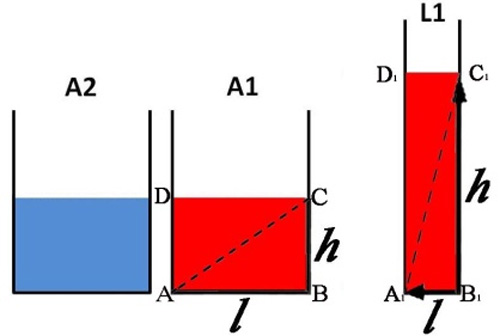
Figure 21 - [de moi] Je reproduis fidèlement – en leurs proportions exactes – les verres utilisés par Piaget pour observer à l’œuvre la « conservation enfantine de la quantité continue ». J’ajoute en plus les symboles « h » (hauteur) e « l » (largeur) et je trace les diagonales AC, A1C1 qui montrent la différence de « pente » entre les verres.

Figure 22 - [de moi] Il suffit, par exemple, de coucher sur le grand côté [A] un rectangle de 12 jetons qu’il a construit en hauteur [L] pour qu’il ne le croie plus équivalent au modèle (dressé). » [Ibid. : 96.]

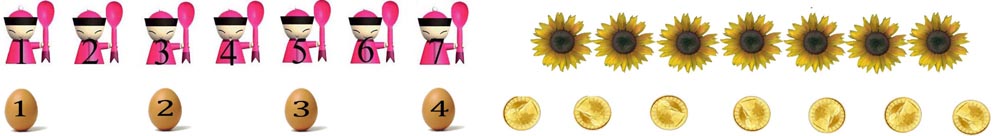
Figure 23 -

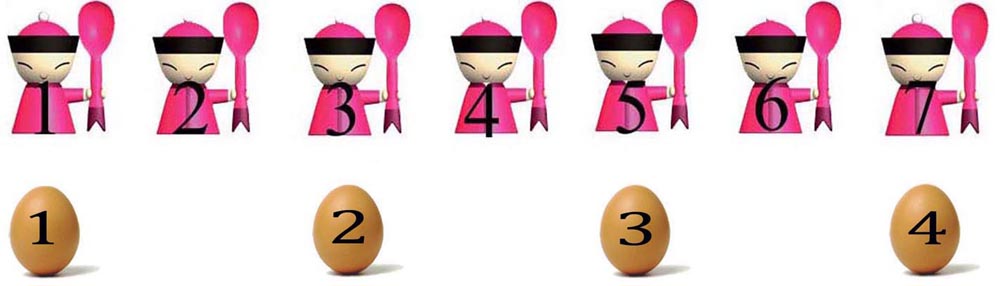
Figure 24 - Si nous regardons cette figure avec les yeux de Cantor, nous ne pouvons pas éviter d’y voir une représentation rigoureuse de l’équipotence entre les nombres impairs 1, 3, 5, 7… et tous les nombres 1, 2, 3, 4…

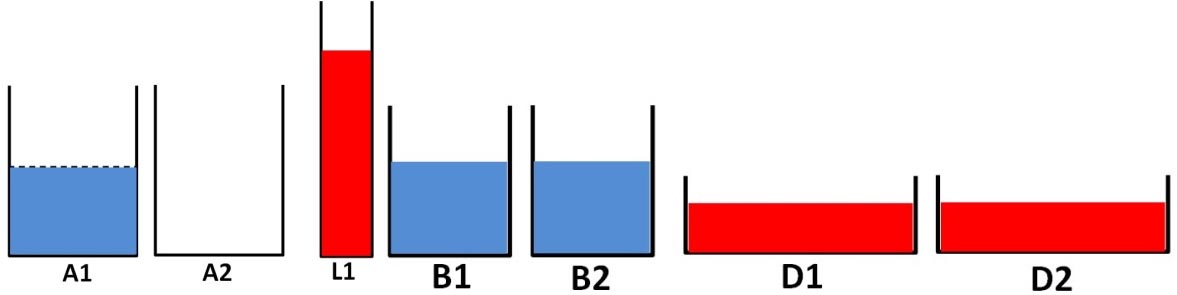
Figure 25 - Et alors si on reverse le bleu et le rouge ici (A2 et A1), le rouge arrivera plus haut ou ce sera la même chose ? — Plus haut. » Sim reverse D1 et D2 en A2 et B1 et B2 en A1 : elle est très étonnée de voir que c'est le même niveau. [Piaget 1941a : 21.]

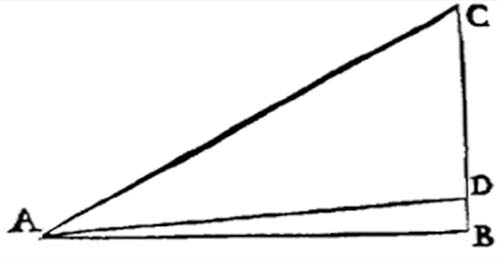
Figure 26 - [Galilée 1632 : 118] Pour se convaincre qu’une même quantité d’élan se conserve dans n’importe quelle inclinaison du plan CA, Sagredo devra accomplir une tâche « [l]×[h] » tout à fait analogue à celle qui trouble l’esprit des enfants interrogés par Piaget. Pour mieux nous en rendre compte, enrichissons l’image galiléenne en considérant les deux plans inclinés A et L, qui reproduisent les proportions des verres en ?62-3? et ?85? :

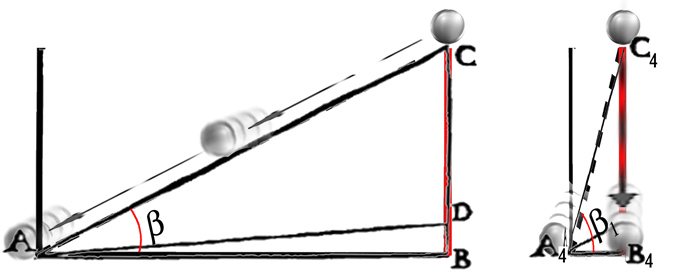
Figure 27 - Si nous comparons les discussions entre Salviati et Sagredo/Simplicio concernant le rapport entre la pente du plan incliné et la quantité d’élan, à celles entre Piaget et les enfants qu’il interroge autour du rapport entre la pente des verres et la quantité de boisson, nous remarquerons l’isomorphisme parfait entre ces deux situations.

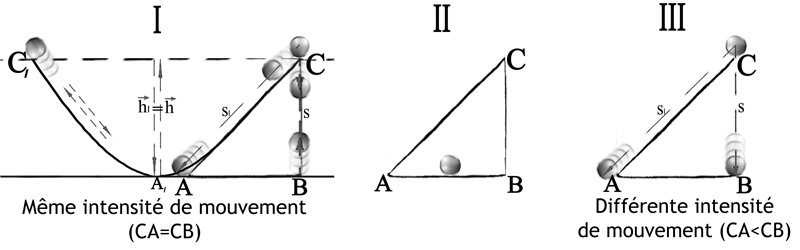
Figure 28 - La maïeutique de Salviati conduit ses interlocuteurs dans la dimension purement projective du phénomène de la chute accélérée, en suivant un rythme ternaire (I-II-III) qui lui permet de tracer une « coupure » à l’intérieur de la notion tout à fait claire et évidente de « vitesse », qui en résulte ainsi subdivisée en une « vitesse-élan » et une « vitesse-rapidité ».

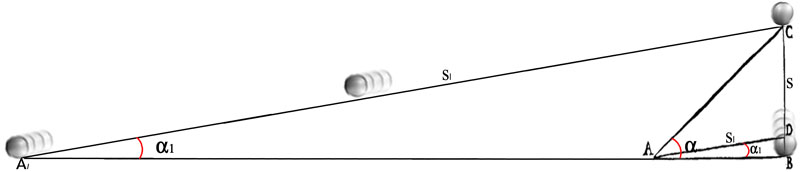
Figure 29 - Un irréductible décalage cognitif oppose l’aspect perceptif d’une évidence mécanique à son essence purement projective. Il nous est beaucoup plus facile de percevoir la lenteur de la bille sur la pente CA1 que sur la pente DA, bien qu’il s’agisse – projectivement – de la même pente S1

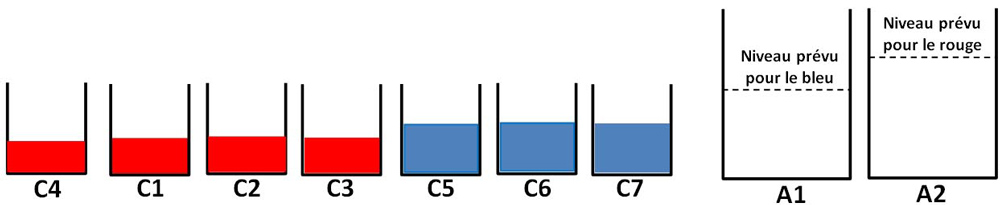
Figure 30 - Sim verse alors elle-même le liquide et constate avec plaisir qu'il s'élève jusqu'à cette marque, mais ensuite elle est fort étonnée en versant le liquide bleu dans A de constater qu'il atteint le même point.) – C'est la même chose ! » [Piaget 1941a]

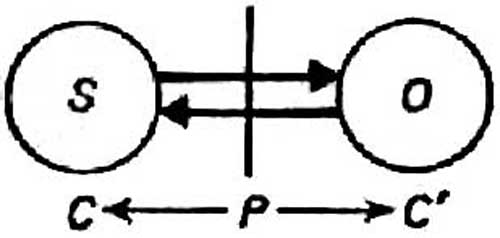
Figure 31 - (99) « La connaissance procède à partir, non pas du sujet, ni de l'objet, mais de l'interaction entre les deux, donc du point P de la figure ci-contre, point qui est effectivement périphérique par rapport tant au sujet (S) qu'à l'objet (0). De là, la prise de conscience s'oriente vers les mécanismes centraux C de l'action du sujet, tandis que la prise de connaissance de l'objet s'oriente vers ses propriétés intrinsèques (et, en ce sens, également centrales C), et non plus superficielles en tant qu'encore relatives aux actions du sujet. Or, comme nous y reviendrons plus loin, les démarches cognitives orientées vers O et vers C sont toujours corrélatives, cette solidarité constituant la loi essentielle de la compréhension des objets comme de la conceptualisation des actions […] Ainsi par un va-et-vient entre l'objet et l'action, la prise de conscience se rapproche par étapes du mécanisme interne de l'acte et s'étend donc de la périphérie P au centre C […]. Les désadaptations se produisent à la périphérie P de l'action, ce qui imprime à la conscience de celle-ci une direction centripète en C, en même temps qu'orientée vers la compréhension de l'objet en C’. » [Ibid. : 263-64.]

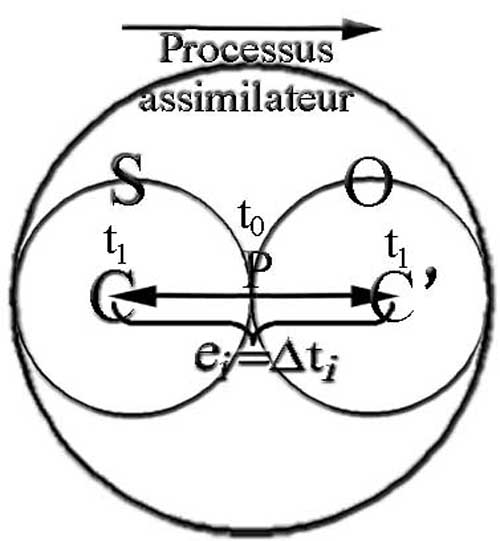
Figure 32 - Un modèle du processus « assimilateur » de la « prise de conscience », selon la façon dont Piaget en décrit la dynamique interne.

Figure 33 - Une perspective de synthèse sur les difficultés de conservation perceptive endurées par les enfants piagétiens, et celles de conservation projective endurées par les interlocuteurs adultes de Salviati, nous montre que dans tous ces cas il est question d’une difficulté de réorientation spatiale d’un cadre cognitif donné.

Figure 34 - Une perspective de synthèse sur les difficultés de conservation perceptive endurées par les enfants piagétiens, et celles de conservation projective endurées par les interlocuteurs adultes de Salviati, nous montre que dans tous ces cas il est question d’une difficulté de réorientation spatiale d’un cadre cognitif donné.

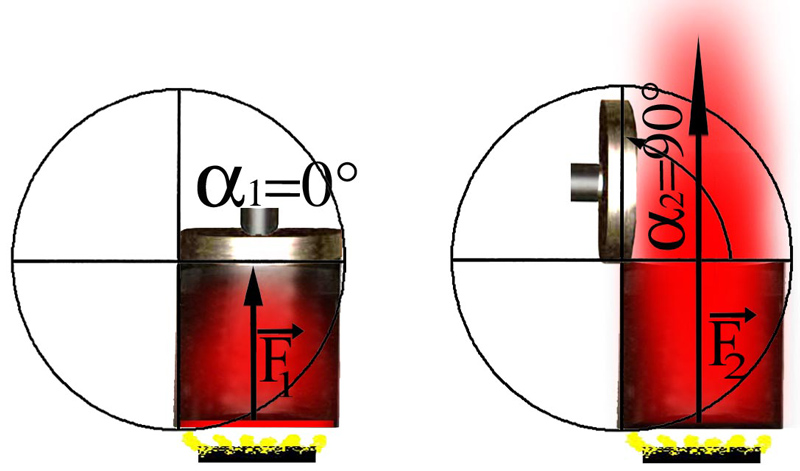
Figure 35 - À la différence du cas de l’enfant avec son bâton à réorienter, lorsqu’il est question d’un engin mécanique fait pour s’ouvrir dès que la vapeur atteint un certain degré de pression, le processus de réorientation (ouverture) du couvercle est univoquement engendré par l’augmentation continue d’une seule et même force imprimée.

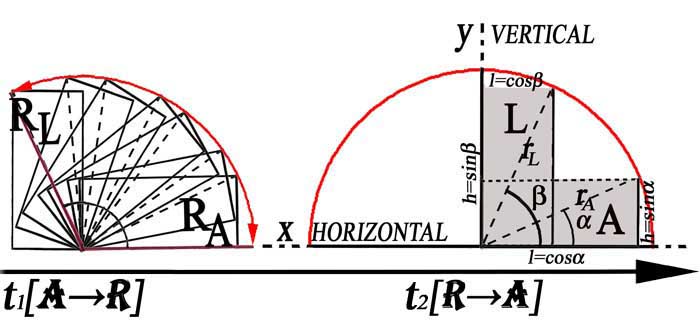
Figure 36 - (a) La conservation perceptive d’une même quantité de boisson lors de son transvasement d’un verre « couché » à un verre « debout » revient à la capacité de synthétiser une situation initiale d’horizontalité et une situation finale de verticalité comme les deux extrêmes d’un seul et même mouvement de rotation. (b) La même chose vaut dans le cas de la conservation purement projective d’une même transformation trigonométrique.

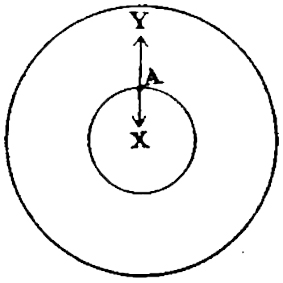
Figure 37 - Soit l'organisme représenté sous la forme d'un petit cercle inscrit dans un grand cercle, lequel correspond lui-même à l'univers ambiant. La rencontre entre l'organisme et le milieu s'opère au point A et en tous les points analogues à la fois les plus extérieurs à l'organisme et les plus extérieurs au milieu lui-même. » [Piaget 1937 : 311.]

Figure 38 - Lorsqu’une même quantité de boisson contenue dans le réservoir A1 est transvasée dans la chaudière L1, elle subit un processus de dilatation qui, en l’occurrence, permet aux trains de marcher. De toute évidence, ce processus est une très exacte répètition in re des « erreurs » perceptives des enfants incapables de conserver la « quantité continue » : c’est « la même boisson » ! Le monde où Lavoisier a institué le principe de conservation du poids des éléments chimiques malgré leurs incessantes transformations est donc un monde où rien n’a l’air de se « conserver », et qui donne tout à fait raison à ces mêmes enfants.

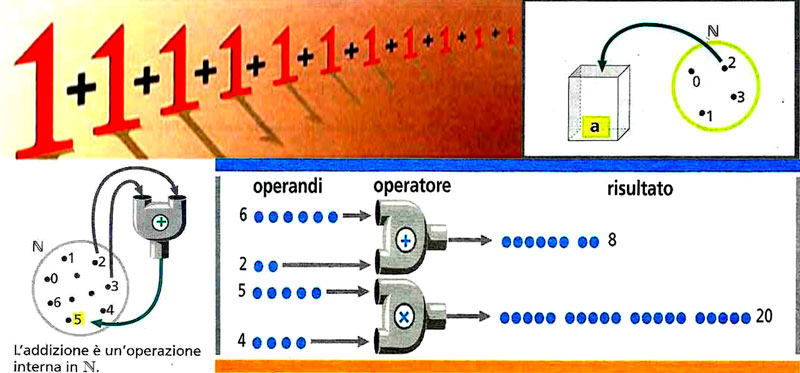
Figure 39 - Selon la didactique actuelle, (a) tout nombre n donné s’explique comme une juxtapposition/accumulation de 1+1+1… ; (b) la lettre censée exprimer la valeur d’une constante est une boîte dans laquelle nous entassons des nombres, donc des 1+1+1… ; (c-d) une opération mathématique est un mécanisme qui introduit des groupes de billes dans une sorte de magique mitrailleuse en métal, qui les crache ensuite en alignement parfait, tout en en gardant la distance mutuelle.

§7.4.2 L’ESPRIT OCCULTE D'EUCLIDE - Pendant la période destinée à l’oubli, affirme Piaget, l’enfant « destiné à la science » croit dans les esprits occultes :

<134>« Les deux premiers stades sont caractérisés par l'absence de toute conduite spéciale relative aux objets disparus. Ou bien le tableau qui s'éclipse entre aussitôt dans l’oubli, c'est-à-dire dans le néant affectif, ou bien il est regretté, désiré et attendu à nouveau, et la seule conduite utilisée pour le retrouver est la répétition simple des accommodations antérieures. Cet univers primitif est phénoméniste, et loin de constituer d'emblée un monde de substances. [...] L'objet disparu n'est pas encore pour lui un objet permanent qui se déplace : c'est un simple tableau qui rentre dans le néant sitôt éclipsé, pour en ressortir sans raison objective. [...] [Quand] l'enfant espère le retour du tableau intéressant (de sa maman, etc.) qu'il lui attribue une sorte de permanence affective ou subjective sans localisation ni substantialisation : le tableau disparu demeure, pour ainsi dire « à disposition », sans qu’il se trouve nulle part au point de vue spatial. Il demeure ce qu'est un esprit occulte pour le magicien : prêt à revenir, si l'on s'y prend bien, mais n'obéissant à aucune loi objective. Or comment l'enfant s'y prend-il pour ramener à lui l'image de ses désirs ? Simplement en criant au hasard ou en regardant l'endroit où elle s'est éclipsée et où elle a été vue pour la dernière fois. » [Piaget 1937 : 17, 16.]

Le « rationalisme géométrique » ne se présente donc, pour Piaget, que lorsque l’enfant « renonce » à des croyances aussi irrationnelles car il peut nous donner raison du « comment objectif » de toute nouvelle apparition. Or, j’affirme que le contraire exact est vrai. Considérons la première Proposition des Éléments d’ Euclide: « construire un triangle équilatéral », et suivons-là du point de vue de l’enfant décrit ci-dessus en <134>.

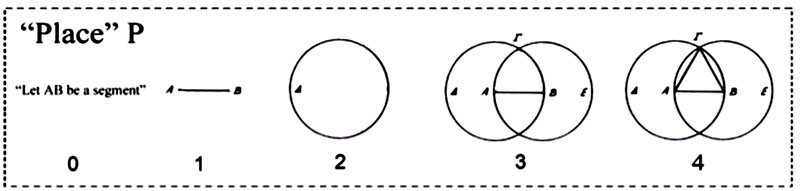
Figure 40 - La première apparition d’un théorème de géométrie dans l’esprit de son créateur est un événement de pure et simple magie enfantine « décalée ».

Ce petit Euclide parlerait ainsi : « Soit P l’endroit du “dynamisme de l'efficace pratique de mon action propre” ». [0-1] « Que le segment AB “sorte du néant” seulement car je désire subjectivement qu’il en soit ainsi. [2] « Que ce même segment AB “s'éclipse dans le vide”, et que le cercle ? apparaisse » [3] Et maintenant, que le segment AB – qui est entre-temps “resté à disposition prêt à revenir” – ressorte du néant “au même endroit P qu'il a quitté en 2, et où mon action propre l’avait trouvé” en 0-1 ; et que le cercle E apparaisse aussi. En outre – et sans aucune raison qui ne soit subjective – je veux aussi que le segment AB soit en même temps le rayon des deux cercles ? et E. [4] « Que les rayons AG et GB jaillissent du néant, et qu’ils aient la même longueur que AB. [Conclusion] « Sans aucune raison objective, et seulement car je l’ai ainsi voulu, désiré et espéré, j’ai été capable de faire apparaître et disparaître, ressortir du néant et s’y re-éclipser, des figures et des images auxquelles j’ai donné les noms que j’ai préféré leur donner. Si vous avez mes mêmes désirs, et que vous voulez ces mêmes choses que je veux, alors vous serez d’accord avec moi pour dire que le triangle ABG est équilatéral ».

Figure 41 - De même que pour Georg Cantor, selon les petit Zu et Fur « sept » et « quatre » sont « le même nombre », tandis que « sept » et « sept » ne sont pas « le même nombre ».

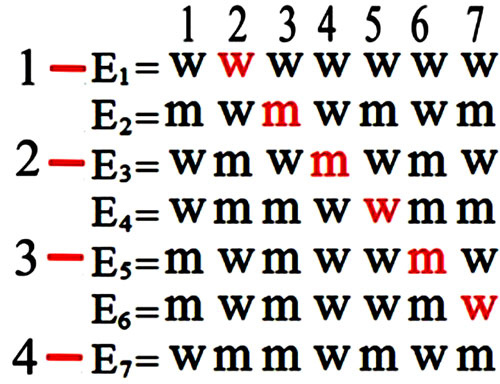
Figure 42 - De même que pour Zu et Fur, selon Georg Cantor « sept… » et « quatre… » sont « le même nombre », tandis que « sept… » et « sept… » ne sont pas « le même nombre ». Ces points de supension disent donc en même temps la puissance dynamique de l’esprit de Cantor, et l’infinité de l’esprit de Zu et Fur.

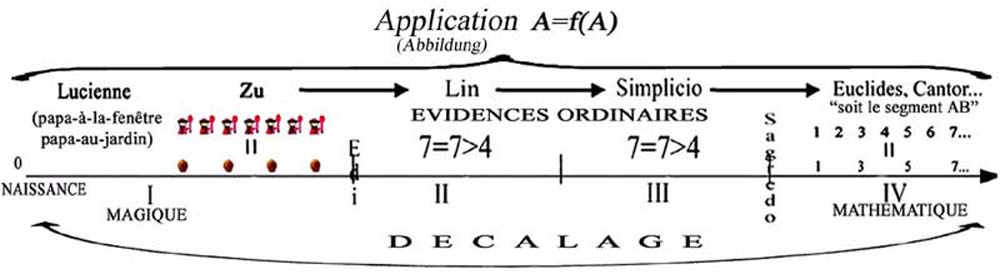
Figure 43 - Un schéma de synthèse de la totalité du développement humain, par « décalages successifs », à partir de notre naissance jusqu’à l’apparition de l’évidence scientifique devant notre esprit. L’essence même des mathématiques et de leur force propulsive (stade IV) est dans les processus « magiques » et purement créateurs de la pensée enfantine (stade I). Pour que cette magie primordiale puisse toutefois nourrir les canaux de la pensée rationnelle, il faut passer par la phase intermédiare des évidences ordinaires (II-III), où toute « magie » paraîtrait, par contre, avoir fait naufrage dans les mécanismes anodins de la pensée computationnelle. Quant au début de ce processus, il est à situer à l’instant 0 de notre naissance, quand nous transformons magiquement le corps d’un autre en notre corps… et vice-versa. Or l’ unité d’une telle transformation globale – du premier souffle inspiré à Galilée/nourrisson à son premier souffle coupé par la magie silencieuse d’un encensoir oscillant dans une église – n’est pas exprimable avec une notion biologique comme celle d’« assimilation » entre deux choses, mais seulement avec la notion archétypique et déjà hautement mathématique de l’« application » d’une chose en son image.

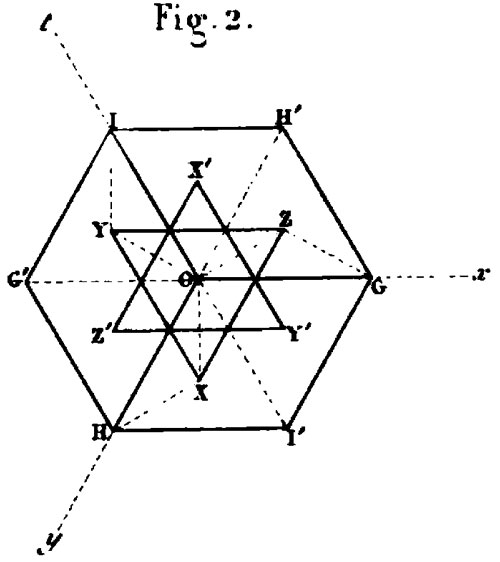
Figure 44 - (140) « Il est admis aujourd'hui, par tous les physiciens, que les corps pondérables sont des agrégations de molécules de même espèce, tenues à distance par des forces attractives ou répulsives dont la résultante est nulle, pour chacune de ces molécules, dès que ces corps sont parvenus à leur état d'équilibre interne. […] Non seulement les molécules d'un cristal sont semblables et semblablement orientées ; mais elles sont, de plus, disposées en files rectilignes, et séparées l'une de l'autre, sur chaque file, par des intervalles égaux. […] Le cristal, ainsi réduit par la pensée, n'est plus qu'un système de points mathématiques distribués, suivant la loi de l'équidistance, sur des files rectilignes parallèles entre elles. Cette définition est précisément celle que nous avons donnée des Assemblages ou Systèmes réticulaires de points. » [Bravais 1866 : 277.]

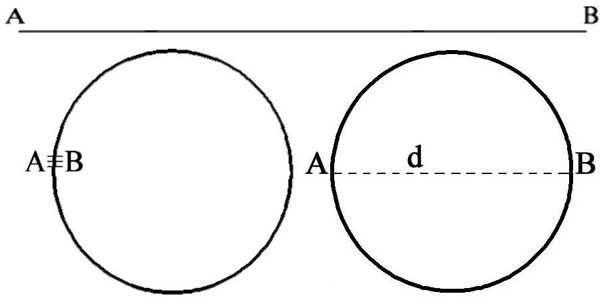
Figure 45 -

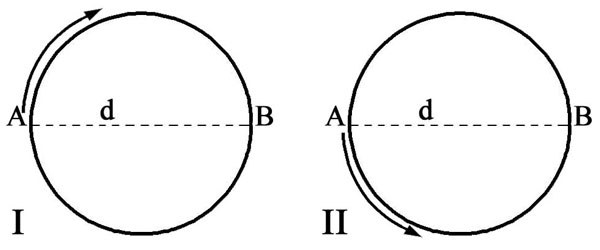
Figure 46 -

Figure 47 -

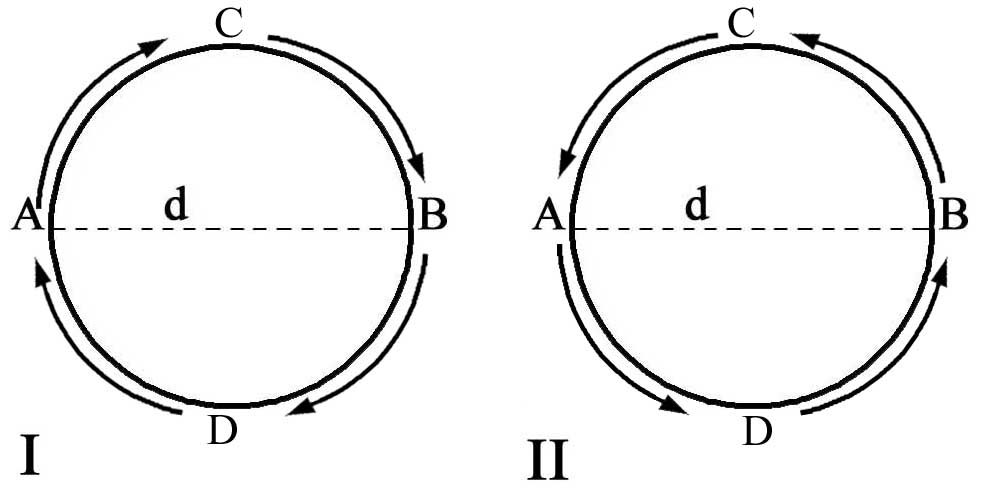
Figure 48 -

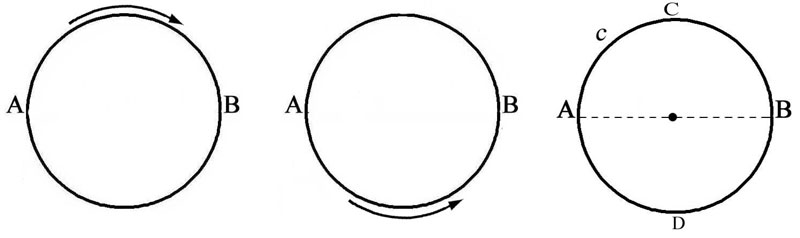
Figure 49 -

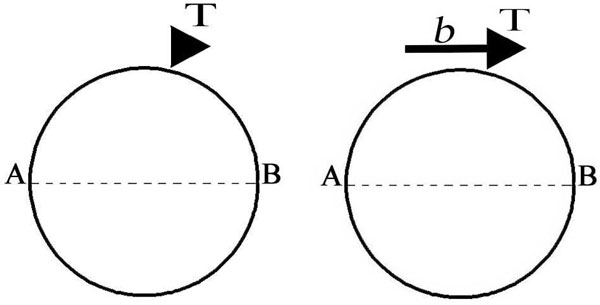
Figure 50 -

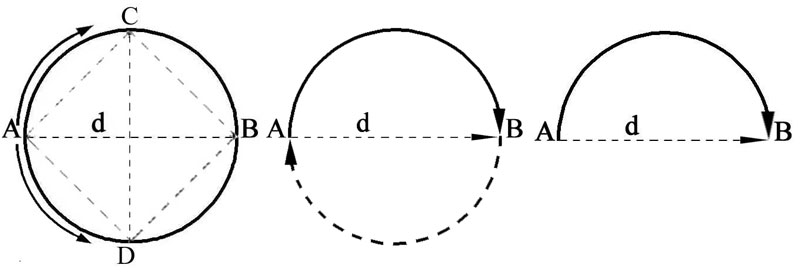
Figure 51 -

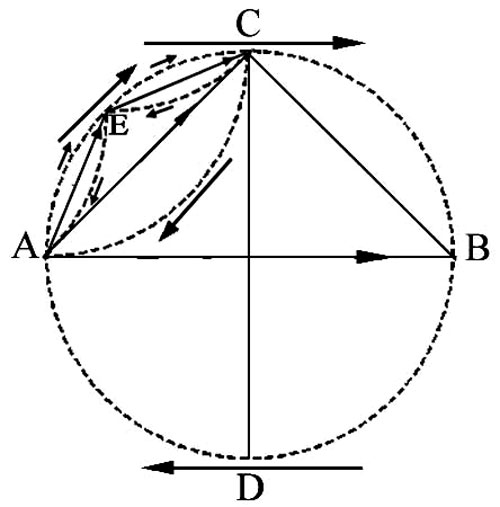
Figure 52 -

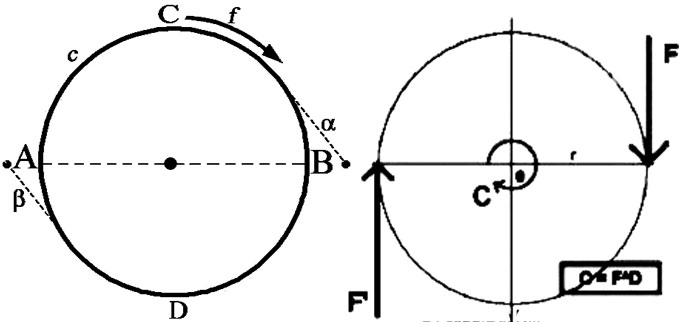
Figure 53 -

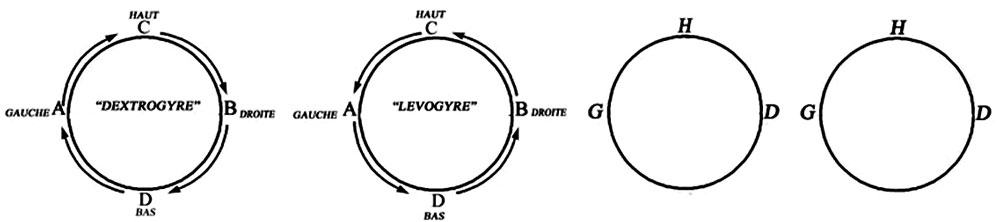
Figure 54 -

Figure 55 -

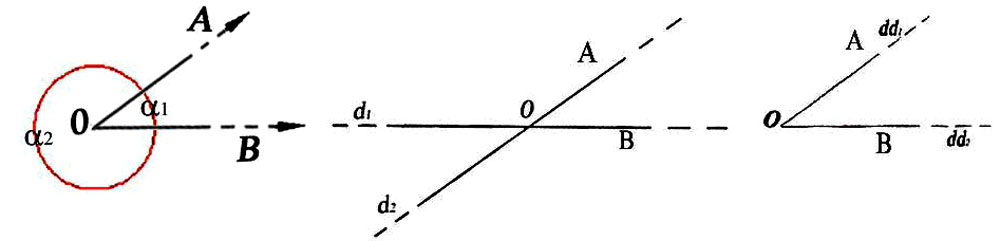
Figure 56 -

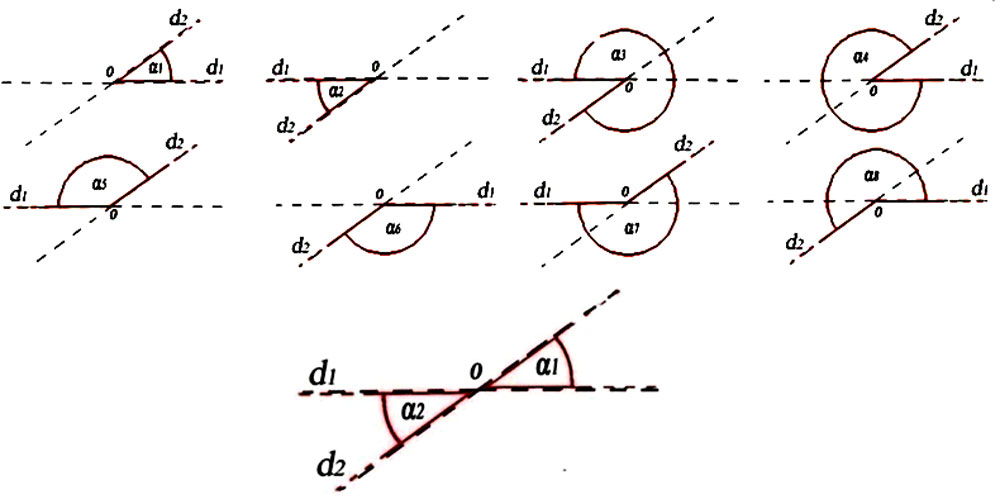
Figure 57 -

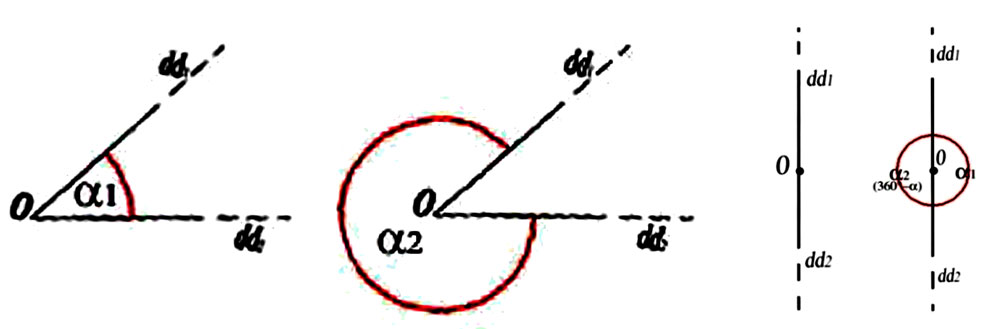
Figure 58 -

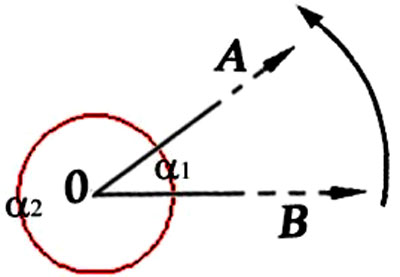
Figure 59 -

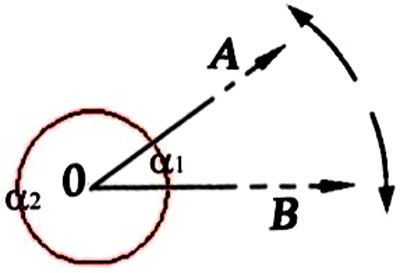
Figure 60 -

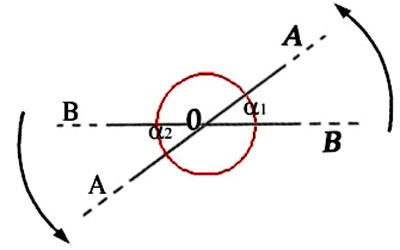
Figure 61 -

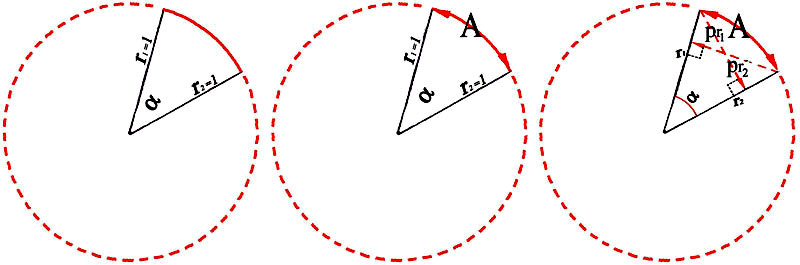
Figure 62 -

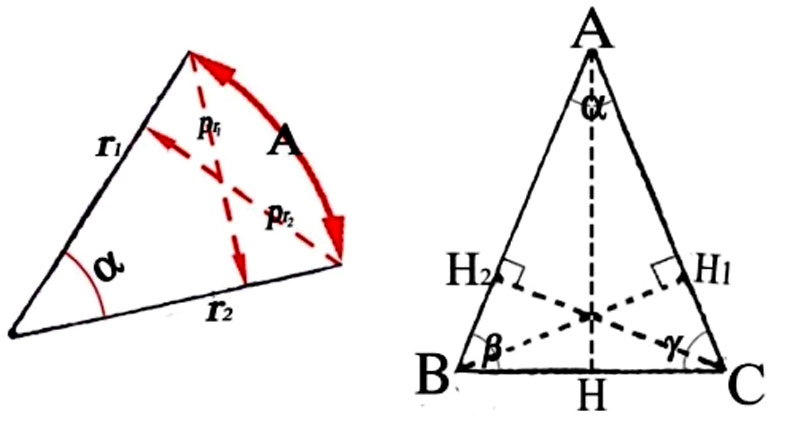
Figure 63 -

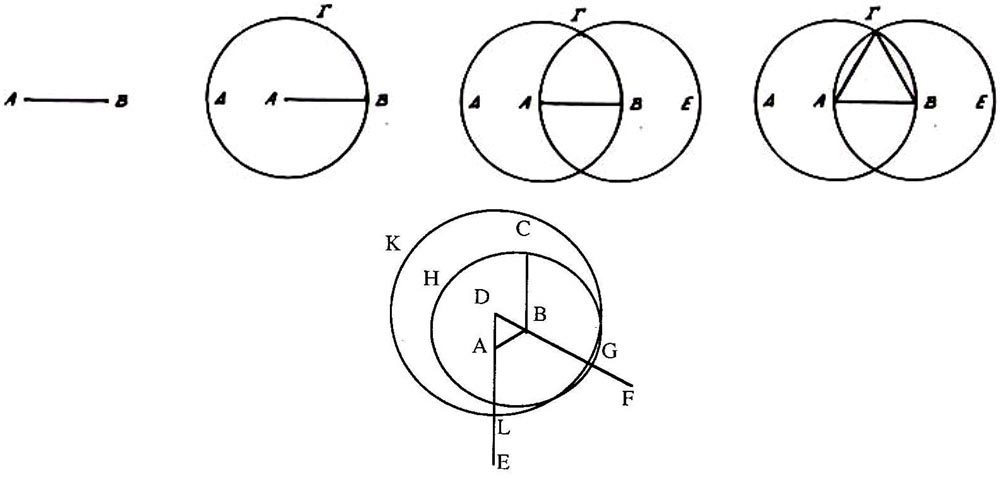
Figure 64 -

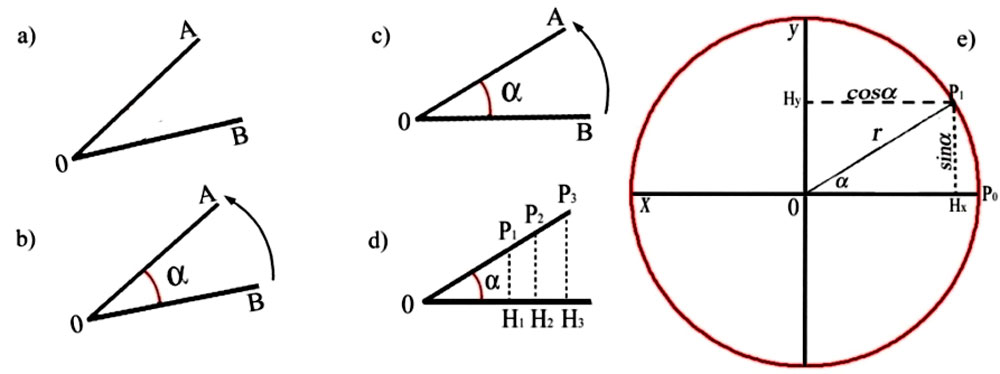
Figure 65 -

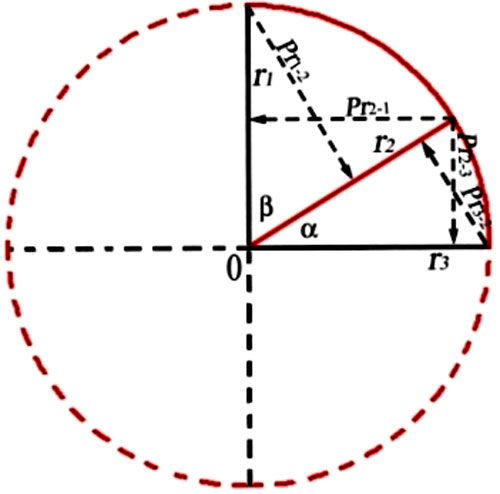
Figure 66 -

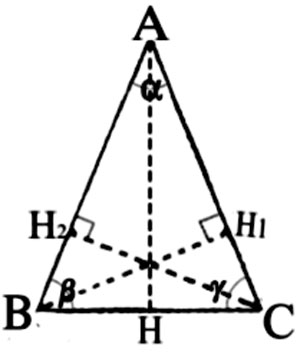
Figure 67 -

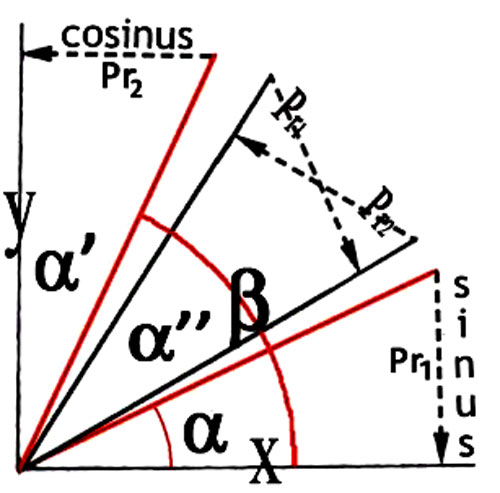
Figure 68 -

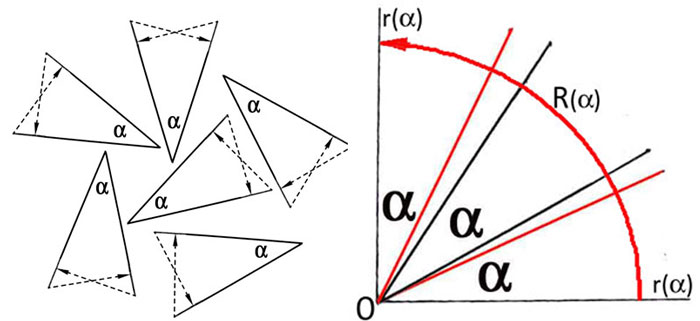
Figure 69 -

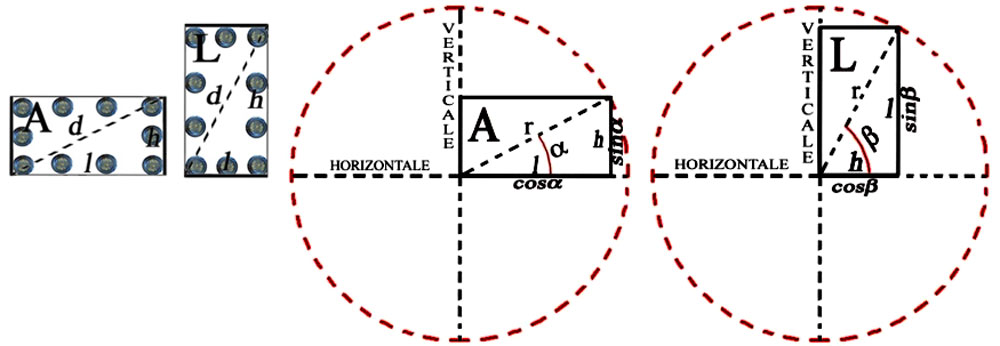
Figure 70 - Blas – I. Un rectangle de jetons A de hauteur h et base l [Fig. 70ab] est saisi par Ba à partir du « seul principe de synthèse » de sa « forme d’ensemble, en tant qu’intuition fondée sur la perception globale de sa figure ». II. Or, cette méthode d’appréhension, qui impose la « prédominance de l’intuition perceptive » distingue absolument entre dressé et couché. Le rectangle A apparaît couché. III. En conséquence de cette irréversibilité, lorsque Ba perçoit le rectangle L=A, mais avec h et l en rapport inversé – à savoir, il saisit le même rectangle, mais dressé – il voit que dans le rectangle dressé il y a plus de jetons que dans le même rectangle couché. IV. Aux yeux de Ba – pour sa vision et pour son esprit – la différente configuration perceptive des deux figures l’emporte donc sur leur égalité euclidienne, et impose enfin une prédominance quantitative « globale » ou « syncrétique » du dressé sur le couché. Sa vision le convainc qu’il y a plus de jetons dans l’un que dans l’autre, même si c’est l’enfant en personne qui vient de réorienter la figure, sans rien changer d’autre. Figure 70ab -cd Pappus – I. Un rectangle euclidien A de hauteur h et base l [Fig. 70cd] est saisi par Pappus à partir du seul principe de synthèse de son appartenance à la forme d’ensemble du cercle trigonométrique, en tant qu’intuition fondée sur la vision projective de cette configuration globale, qui perçoit h comme sina?, l comme cosa? et d comme r. – II – Or, cette méthode d’appréhension, qui impose la prédominance de l’intuition projective de l’espace trigonométrique, distingue absolument entre axe vertical et axe horizontal. La base l = cosa du rectangle apparaît placée sur l’axe horizontale, tandis que la hauteur h = sina?apparaît placée sur l’axe verticale. III – En conséquence de cette irréversibilité, lorsque Pappus perçoit le rectangle L=A, mais avec la hauteur h= cosß?et la base l = sinß??– à savoir le même rectangle euclidien mais réorienté, avec la hauteur h sur l’axe horizontal et la base l sur l’axe vertical – il voit que dans le rectangle avec la base redressée il y a plus d’ampleur que dans ce même rectangle avec la base couchée sur l’horizontale. IV Aux yeux de Pappus – pour sa vision et pour son esprit– la différente configuration projective des deux figures trigonométriques l’emporte donc sur leur égalité euclidienne, et impose enfin une prédominance quantitative, en termes d’ampleur, de la verticale sur l’horizontale. Sa vision le convainc qu’il y a plus d’ampleur dans l’un que dans l’autre, même si c’est Pappus en personne qui vient de réorienter le rectangle A = sina/cosa??en en faisant le rectangle L= sinß/cosß?? A.

Troisième ¨Partie - Redonner une voix à l'homme

<168> [1] ALBERT EINSTEIN « Pour la pensée physique, comme pour la pensée scientifique en général, il est caractéristique qu’elle s'efforce, en principe, de se tirer d'affaire uniquement avec les notions de “nature spatiale” et d'expliquer à leur aide tous les rapports ayant le caractère de loi. Le physicien cherche à réduire les couleurs et les sons à des vibrations, et le physiologiste la pensée et la douleur à des processus nerveux, de telle sorte que le psychique comme tel est éliminé de l'enchaînement causal de l'être et ne se manifeste, par conséquent, nulle part comme lien indépendant dans les liaisons causales. Cette attitude, qui considère en principe comme possible de saisir tous les rapports en employant exclusivement des notions de “nature spatiale” est bien ce qu'on entend actuellement par “matérialisme” (après que la “matière” eut perdu son rôle de notion fondamentale). [2] Je veux seulement dire encore ce que signifient mes paroles quand je dis que nous devons essayer de coller à la réalité physique. Nous sommes tous conscients de ce qui va se révéler être les concepts fondamentaux de la physique. La masse ponctuelle, ou la particule, n'en fait certainement pas partie ; le champ, au sens de Faraday et de Maxwell, peut-être, mais ce n'est pas certain. Mais ce que nous imaginons exister (être “réel”) doit être localisé de quelque manière dans le temps et dans l'espace. » [Einstein 1954a :156 ; Einstein à M.Born, le 18.3.1948, in Born 1972 :180] NORBERT WIENER – [3] « The mechanical brain does not secrete thought “as the liver does bile”, as the earlier materialists claimed, nor does it put it out in the form of energy, as the muscle puts out its activity. Information is information, not matter or energy. No materialism which does not admit this can survive at the present day. » [Wiener 1965:132]

Il est évident que la synthèse entre les mots d’Einstein en <168[1][2]> et les mots de Wiener en <166> et <168[3]> nous renvoie bien plus à une idée, une intention – purement « iconologique » comme celle du Programme de Félix Klein – qu’à une « matière » effectivement saisissable à l’intérieur des propos et des comptes rendus « protocolaires » de ces savants qui en arrivent, en effet, toujours à se débarrasser de la question en l’exilant « to the limbo of badly posed questions » (<166>). En somme, la « matière » du matérialisme est un programme culturel toujours explicitement avoué comme tel, et si on veut effectivement la prendre en charge dans un discours qui distingue entre le oui et le non, il faut tout d’abord en stabiliser les sens, ce que je ferai dans les paragraphes qui suivent. D’autre part, loin de moi l’idée que la dispute entre scientifiques se réduise à une discussion sur le sens des mots, car ceci n’en est que la phase préliminaire. Le oui et le non sont décidés par la pensée expérimentale, qui n’a à faire qu’avec la voix des phénomènes que nous allons donc réentendre dans le prochain chapitre.

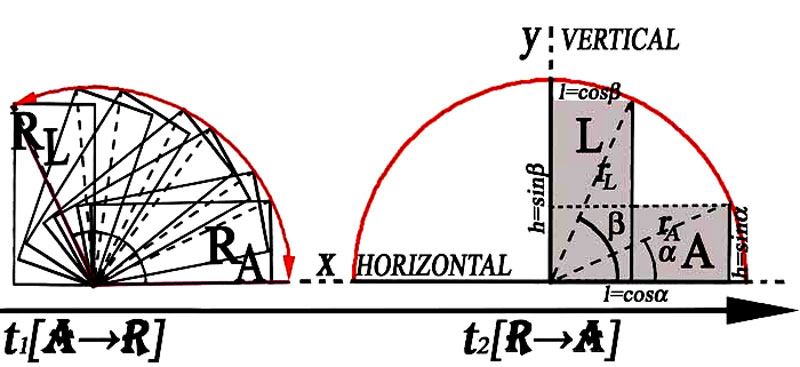
Figure 71 - Notre évolution globale suit le vecteur rigoureusement orienté perceptif-->projectif [cf. Fig. 36] qui est pourtant intérieurement rythmé selon la suite commutative Absolu?Relatif/Relatif?Absolu, car aucune trigonométrie ne pourrait suivre la relationnalité euclidienne des « évidences ordinaires », si l’absoluité du « dressé » et du « couché » qui caractérise le monde perceptif de l’enfance pré-géométrique ne réapparaissait pas pour orienter le monde projectif de l’âge adulte de la science.

Figure 72 - Si nous bloquons les sphères centrales BCD, il devient évident que leur espace immobile est, dans le cas (B), le théâtre d’un mouvement purement potentiel.

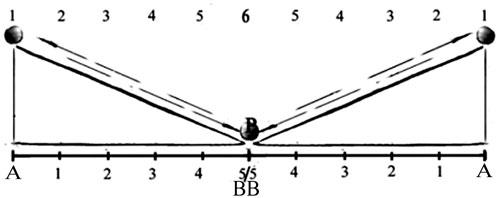
Figure 73 - (225) « SAGREDO : [1] Je crois avoir très bien compris. Supposons que le mouvement commence en partant du repos et que sa vitesse croisse successivement par des ajouts égaux, comme cela se passe avec la suite des nombres à partir de l'unité, et même du zéro qui représente l'état de repos. [2] Disposons-les ainsi, en en plaçant à la suite l'un de l'autre autant que nous voulons, le degré le plus petit étant zéro et le plus grand 5 par exemple, tous ces degrés de vitesse avec lesquels le mobile s'est mû font une somme de 15 ; or, si le mobile se mouvait avec un même nombre de degrés, mais chacun égal au degré maximum, soit 5, l'agrégat de toutes ces vitesses serait le double de l'autre, soit 30 ; si donc le mobile se mouvait aussi longtemps, mais avec une vitesse uniforme égale à celle du degré maximum, 5, il devrait parcourir un espace double de celui qu'il parcourut dans le temps de l'accélération qui commença en partant du repos. » [Ibid. : 367-368]

Figure 73' -Le plan incliné « au miroir », enrichi du « pendule potentiel », et d’une clochette au centre, qui sonne à chaque passage de la sphère roulante/oscillante. La suite régulière des retentissments de la clochette a lieu dans un espace purement potentiel, c'est-à-dire dans le temps.

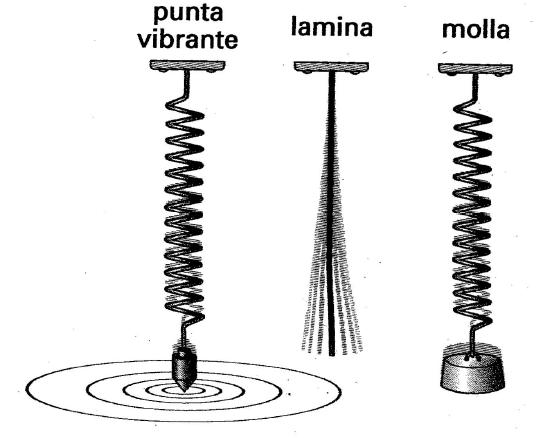
Figure 74 - (228)« [Fig. 74] Objets qui peuvent osciller d’une position d’équilibre, en engendrant des ondes. Dans des conditions données, des corps vibrants/oscillants peuvent sans aucun doute produire le phénomène cinématique d’une « onde ». Cela ne signifie pas, pour autant, que toute « onde » est produite par un corps vibrant/oscillant. QUESTIONS ET RÉPONSES - Comment peut-on engendrer une onde ? Les ondes sont produites par des corps qui oscillent. » [Ruffo : 396, 413]

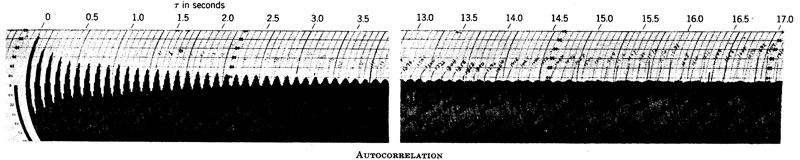
Figure 74' - That such a phenomenon may actually take place in the generation of brain waves for the individual whose autocorrelation is shown in [ici] Fig. 74'. » [Wiener 1965: 179, 198-199. L’italique est de moi.]

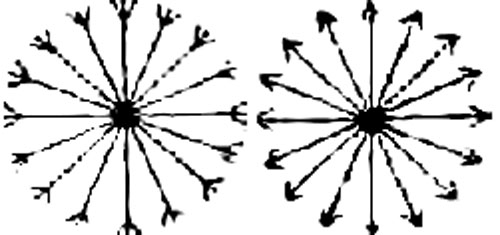
Figure 75 - "Pratyak chetana » et « Parànga chetana" (253) « “Tatah pratyak chetana adhigamo 'py antarâyâbhâvash cha.- De cela [de la répétition et méditation du OM] (résulte) la disparition des obstacles et le retournement vers l'intérieur de la conscience.” – Pratyak Chetanâ est la conscience tournée vers l'intérieur ou la conscience dirigée vers son centre. C’est donc le contraire exact de Parânga Chetanâ, la conscience tournée vers l'extérieur comme les figures suivantes le montrent. Le but et le processus entier du Yoga consiste à retirer la conscience de l'extérieur pour l'amener vers le dedans car le mystère ultime de la vie est caché au cœur même ou centre de notre être. » [Patanjali I : 29 ; Taimni : 78]

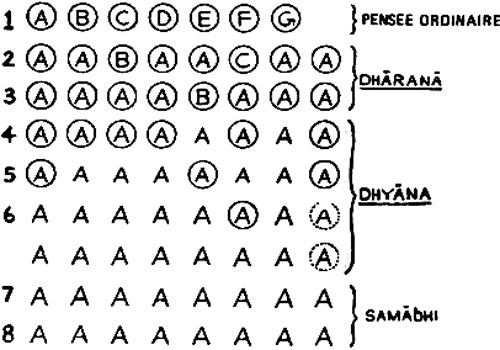
Figure 76 - Les trois étapes finales de l’ashtanga yoga de Patanjali (IIIe siècle avant J.C.). « Dharana » : notre « pensée ordinaire » arrive à se mantenir bien fixe (« defixa », dit Descartes) dans le périmètre d’un seul endroit mental. À l’intérieur de ce périmètre pourtant, l’identité de l’objet de son application attentive – « vitarka » : ici c’est lorsque la lettre est encerclée – est encore instable. « Dhyana » : l’identité de l’objet de notre attention appliquée se stabilise enfin, mais seulement si nous ne « lâchons » pas (d’où les lettres encerclées, qui signalent cette même application récurrente de notre attention). « Samadhi » : l’identité de l’objet de la pensée a totalement reflué dans la pure et simple identité de la pensée même, qui n’a plus aucun besoin de s’« appliquer » pour garder sa présence éveillée. Lorsque cette tradition yogique se focalise sur les mathématiques (Brahamagupta, VIe siècle après J.C), ce dernier moment de « svarupa sunyo » (« vidé de sa propre forme ») s’exprime avec la fraction 0/0, qui est donc le symbole le plus riche en potentialité germinatrice. Pour notre technologie mathématique, en revanche, ce même symbole est, naturellement, « totalement dépourvu de sens ».

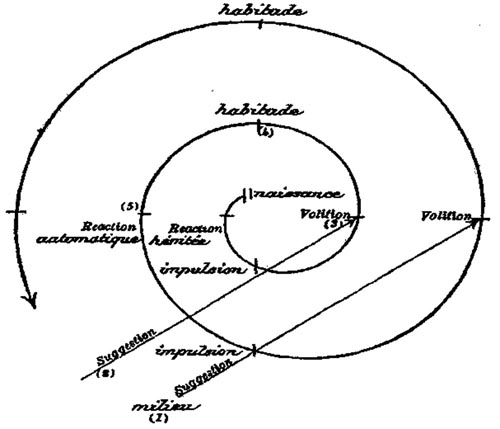
Figure 77 -(259)« Tout d'abord Helen commence par une succession chaotique de mouvements inefficaces. Elle n'aboutit qu'après des insuccès répétés et décourageants, et sans autre mobile agréable que celui de réussir. Si, dans ces expériences motrices elle ne recherchait que le plaisir que donne le mouvement, pourquoi ceux-ci plutôt que d'autres ? Pourquoi poursuivre un résultat qu'elle n'atteignait jamais ? Dans les cas d'imitation persistante, nous avons autre chose et davantage qu'une association. Les mouvements imités sont nouveaux ainsi que les combinaisons qu'ils réalisent. […] Pour cette raison, je suis persuadé que l'imitation persistante constitue bien le processus capital de la volition. […] Au point de vue physiologique, étant donnée la fatigue que produit la combinaison de l'équilibre de la gomme, nous pouvions nous attendre à une diminution de l'énergie, et nous pouvions en conclure que l'enfant se contenterait de réactions purement suggérées s'exprimant par les anciens canaux d'expression. Mais il n'en est rien : l'enfant ne se tient pour satisfait que lorsqu'il est arrivé à produire une nouvelle réaction de la sorte particulière du modèle. Nous devrons donc supposer que chaque effort, au lieu d’épuiser son énergie, produit un accroissement des processus physiologiques et favorise la sélection de son expression motrice et ainsi de suite jusqu'à ce que le modèle soit parfaitement imité. […] Ainsi la vie se prolonge, s'élargit et s'agrandit. Je me suis servi de la spirale pour marquer la continuité du progrès durant cette période, de même que je m'en sers encore pour schématiser le progrès de la race [Fig. 77]. » [Baldwin 1895 : 347-349]

Figure 78 - (269) « Le nombre d'or de l'écriture - Marc Changizi et son collègue Shinsuke Shimojo ont étudié en détail l'organisation visuelle de chacun des caractères de 115 systèmes d'écriture de tous styles et de toutes époques, allant du linéaire B de l'ancienne Crète au runique en passant par l'étrusque ou l'alphabet phonétique international. PREMIERE REGULARITE MAJEURE que le lecteur vérifiera aisément en Fig. 78 : presque tous les caractères sont formés d'environ trois traits (des courbes que l'on peut dessiner sans arrêter ni lever le crayon), avec une variabilité assez faible : que l'on pense à nos lettres T ou P (2 traits), F ou N (3 traits), M ou W (4 traits). Si une écriture nécessite plus de caractères – l'étrusque en compte 23, l'alphabet phonétique en dénombre 170 – , les nouveaux caractères sont formés en créant de nouveaux traits de base afin de conserver toujours environ trois traits par caractère. […] D'où provient ce nombre magique d'environ trois traits par caractère ? Il correspond au taux d'accroissement de complexité des neurones du cortex visuel : nous avons vu qu'à chaque étape, le champ récepteur augmente d'un facteur 2 ou 3 tandis que s'accroît d'autant l'invariance et la taille des unités représentées. Ainsi, chaque caractère aurait une forme essentiellement optimale pour être aisément reconnaissable, par un neurone unique du cortex temporal ventral, comme une combinaison de deux, trois ou quatre courbes du niveau inférieur. Il serait même tentant de prolonger l'analyse de Changizi et Shimojo à d'autres niveaux. Un cran plus bas dans la hiérarchie visuelle, il est plausible que les traits fondamentaux eux-mêmes soient reconnus comme conjonction de deux, trois ou quatre segments de droite. Un cran plus haut, au moins dans les écritures alphabétiques, on constate que la plupart des unités composées de plusieurs lettres – racines des mots, préfixes, suffixes, terminaisons grammaticales – font presque toujours deux, trois ou quatre lettres de long. De même en chinois, la majorité des caractères sont formés par la combinatoire de deux, trois ou quatre marqueurs sémantiques et phonétiques. Sur le plan visuel, toutes les écritures semblent donc fondées sur une grande pyramide hiérarchique dont le nombre d'or est 3, plus ou moins 1. » [Dehaene 2007 : 236, 237. L’italique est de moi.]

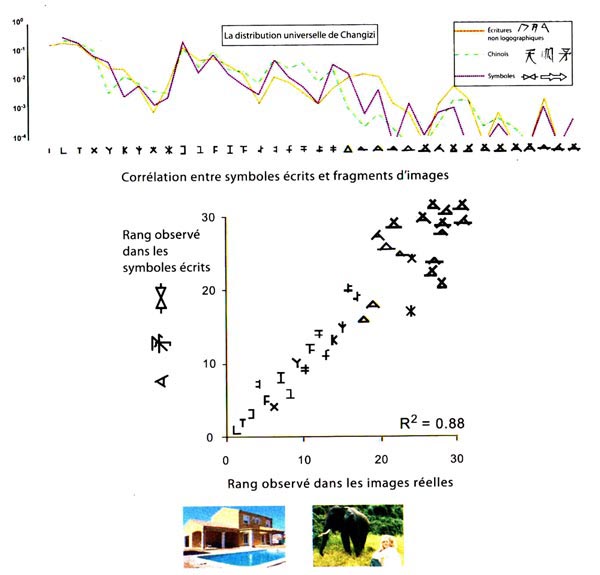
Figure 79 - (270) « SECONDE REGULARITE MAJEURE : les configurations de traits qui forment les caractères sont très reproductibles. Dans toutes les écritures, leur fréquence suit une loi universelle qui reproduit celle que l'on peut observer dans la nature. – Pour comprendre cette loi, examinons ensemble comment les différents traits se rejoignent au sein d'un caractère. Deux traits peuvent former un T, un L ou un X ; trois traits peuvent former de nombreuses configurations en F, K, Y, A... Considérons ces configurations d'un point de vue purement topologique, sans tenir compte de leur possible distorsion ou de leur orientation sur la page, et comptons combien de fois survient chacune d'entre elles. Une élégante régularité émerge : dans toutes les écritures du monde, le profil de fréquence des configurations est le même. En particulier, le L et le T sont plus fréquents que le X ; le F est à peu près aussi fréquent que le X, et bien plus fréquent que le Y ou le A. D'où provient cette distribution universelle ? Elle n'est en rien le résultat du hasard : si l'on jette, sur un plan, des segments de droite, leurs intersections ne sont pas réparties selon la distribution observée par Changizi. En revanche, on retrouve cette distribution lorsqu'on analyse les statistiques des images du monde extérieur, qu'il s'agisse de scènes de la nature ou de la vie urbaine. Lorsque plusieurs objets se rejoignent, se masquent ou se superposent, leurs contours forment des configurations caractéristiques où dominent des formes simples comme le T ou le L. Le X n'y est pas si fréquent, sauf lorsqu'une fine branche passe devant un autre contour. Le A est plus rare encore dans les scènes naturelles. Lorsqu'on compile des centaines d'images, le nombre de configurations de chaque type que l'on observe corrèle très étroitement avec la distribution universelle des symboles écrits. » [Dehaene 2007 : 239. Les italiques sont de moi.] Non seulement, donc, notre esprit narrateur n’écoute dans le monde que la fréquence de ses horloges retentissant dans la voix de tout événement identifiable… mais encore, ce même monde s’avère peuplé de « protolettres », qui brillent à la racine de la totalité de nos alphabets : ?271? « Partout sur notre planète, lorsqu'ils ont eu l'idée de noter la langue par écrit, les hommes ont convergé, par essais et erreurs, vers les formes caractéristiques des « protolettres » dont on a vu qu'elles sont déjà codées au plus profond du cortex temporal ventral des primates. En définitive, l'analyse des écritures du monde souligne, avec une grande force, que leur forme ne résulte pas d'un choix culturel arbitraire. Le problème de la communication écrite est tellement contraint sur le plan cérébral qu'il ne laisse guère de place au relativisme culturel. Notre cerveau de primate n'admet qu'un petit jeu de formes écrites. » [Dehaene 2007 : 239]

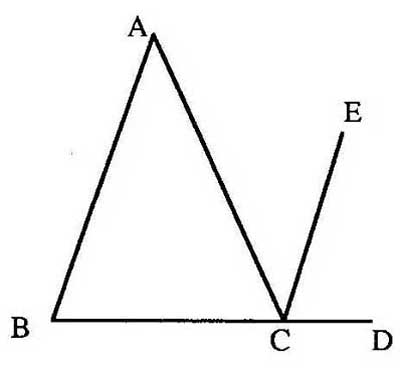
Figure 80 - (282) « [1] Étant donné le triangle ABC [Fig. 80], le couple de parallèles AB//CE et la droite CD colinéaire à BC, il s’en suit que [2] comme BAC=ACE puisqu’alternes internes, et (3) que ABC=DCE puisque correspondants externes, alors [4] les trois angles internes CAB, ABC, BCA sont équivalent au trois angles adjacents BCA, ACE, ECD en ce que [5] ajoutant une même chose (BCA) à deux choses égales (CAB,ABC ; ACE, ECD) le résultat est le même. Mais [6] BCA, ACE, ECD = 2droits, donc [7] BCA, CAB, ABC =2droits. » [Synthèse d’Euclide, Élém. I, 32] - (283) « [1] Prenons deux grandeurs (abstraites) quelconques, par exemple 5 et 12 [AB et C en Fig. 83]. [2] Il est évident que l'ensemble des grandeurs comprises entre 0 et 5 (ou qui sont inférieures à 5) est infini ; de même l'ensemble des grandeurs inférieures à 12. [3] Il n'en est pas moins certain que le deuxième ensemble doit être dit plus grand que le premier, puisque celui-ci n'en est incontestablement qu'une partie. [4] [Donc il est possible qu’une grandeur infinie soit plus grande qu’une autre]. » [Bolzano : 87. Les insertions entre crochets sont de moi.]

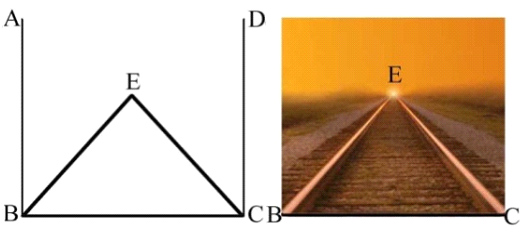
Figure 81 - Sur la surface évidente des phénomènes, les parallèles AB et CD ne convergent pas. Ceci est une vérité postulée avec une force tellement impérative, que notre perception se charge elle-même de feindre un espace de profondeur, pour qu’un tel événement absolument impossible puisse avoir lieu. La même chose se passe au niveau de nos projections dans la profondeur purement intellectuelle de la sphère riemanienne.

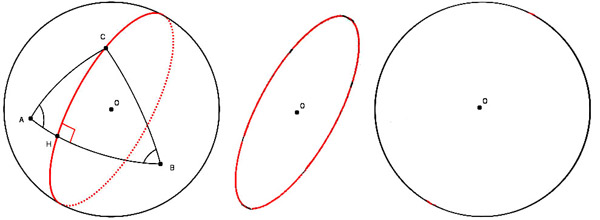
Figure 82 - Un cercle n’est pas une ellipse. Cette vérité euclidienne est tellement absolue, que notre perception se charge elle-même de feindre la troisième dimension d’une sphère ou d’un « disque volant », lorsque nous décidons activement que ce même cercle et cette même ellipse sont (ou appartiennent à) une seule et même chose.

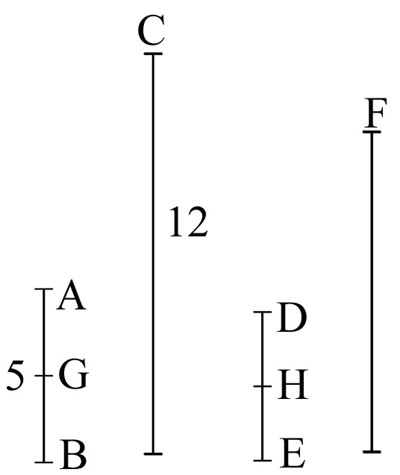
Figure 83 - Euclide présuppose de toute évidence qu’il nous est donné de dire : cette partie AB de C et cette partie DE de F sont « la même partie ». Nous savons toutefois – car nous connaissons les nombres 1, 2, 3… – que cette « même partie » ne nous met pas à disposition un nombre qui fait partie de cette même suite actuellement disponible, et cela car les parties-de-nombre AB=DE (appelons-les Q’) ne « mesurent » pas les nombres C et F dont elles font partie. Pour réaliser la comparaison nous devons toutefois, d’une manière ou d’une autre, accéder au « nombre » que AB et DE représentent en ce qu’elles sont bien des parties (entre elles équivalentes) d’une totalité numérique. C’est à ce point qu’Euclide prend la seule route disponible : celle qui ne nous conduit pas de la partie au tout – car ces parties ne mesurent pas le tout dont elles font partie – mais du tout à la partie, car à la différence du chemin partie ? tout, pas toujours disponible, le chemin tout ? partie « doit pouvoir » être parcouru.

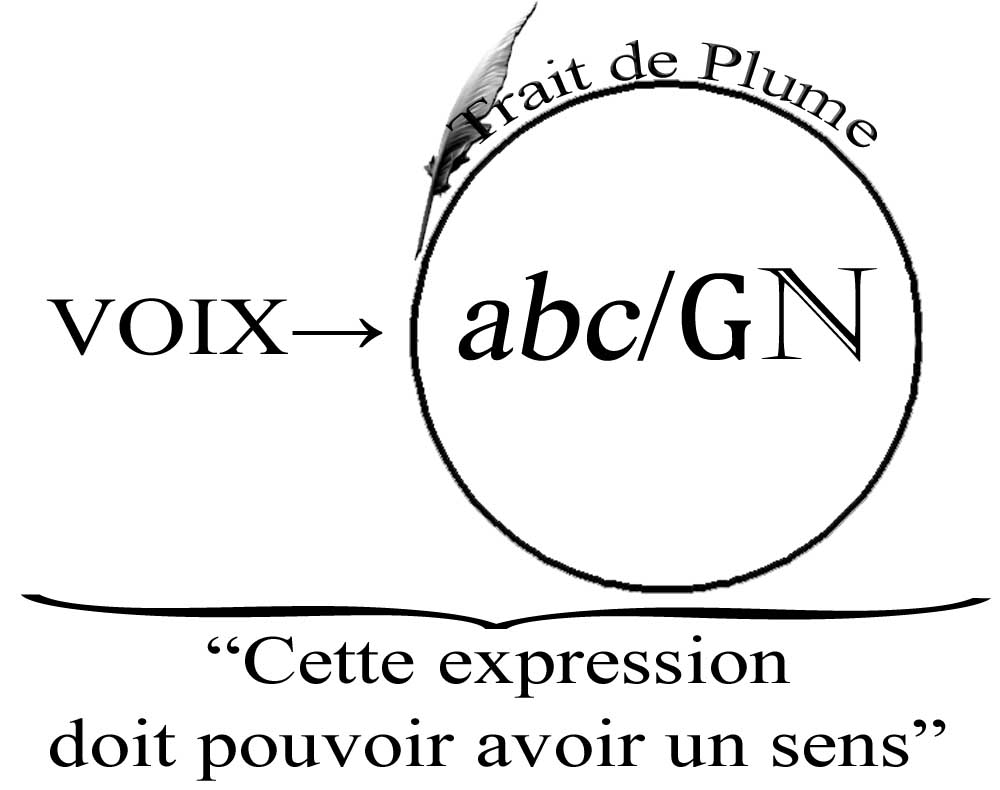
Figure 83' - À l’école, c’est notre voix – soit-elle « muette » ou retentissante – qui transforme le « trait de plume » en des expressions nécessairement susceptibles de nous révéler leur sens. Ce n’est qu’une fois que ce champ unitaire et homogène s’est formé devant notre conscience, que nous pouvons tracer une diaïresis distinguant entre le trait-de-plume des lettres et le trait-de- plume des nombres/grandeurs. Encore une fois, donc, une même force – la force exercée par le postulat « ceci doit pouvoir avoir un sens » – s’avère procéder par émanations successives, productrices d’un enchaînement orienté de « coupures » qui instituent, au fur et à mesure, les dimensions fondatrices de notre expérience herméneutique du monde.

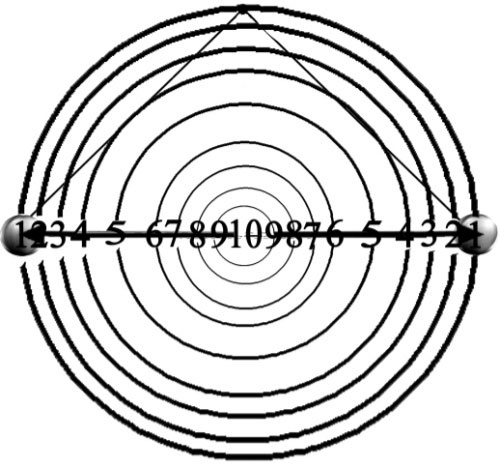
Figure 84 - Le « diamètre de Salviati ». Le pendule chute en traçant un demi-cercle dont le diamètre est la ligne où se succèdent les projections successives des vitesses croissantes/décroissantes atteintes par la sphère oscillante. Ces vitesses se trouvent donc, à leur tour, aux extrêmes diamétraux d’une suite de [demi]cercles successifs et concentriques.

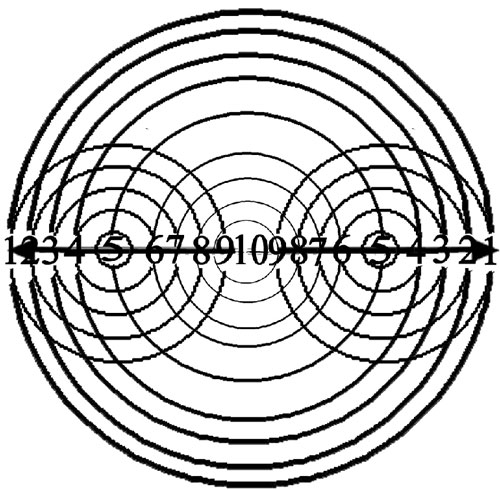
Figure 85 - Le « diamètre de Sagredo ». Même à l’intérieur de l’un des deux rayons du « diamètre de Salviati », nous pouvons choisir n’importe quel point/vitesse (ici le 5), pour voir se répéter la même loi arithmétique de « correspondance diamétrale » observée dans le cas du « diamètre de Salviati ».

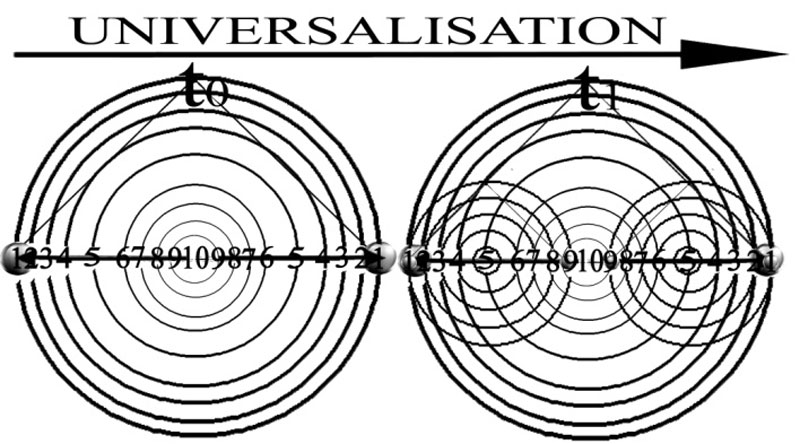
Figure 86 - Le passage du « diamètre de Salviati » – directement évident et saisissable, sur la surface immédiate du dessin à gauche – au « diamètre de Sagredo » à droite – qui, au contraire, doit être repéré sans la profondeur de ce même dessin – a la nature d’un mouvement d’universalisation, grâce auquel Sagredo saisit la présence d’une seule et même forme à la racine de cette double phénoménologie.

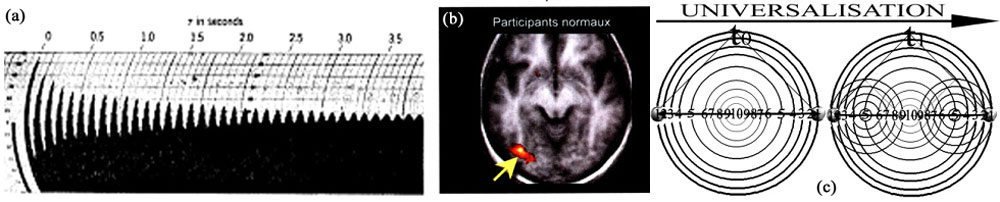
Figure 87 - Ainsi que toute autre évidence mathématique symboliquement exprimée grâce à un « trait de plume », la figure en (c) a la nature d’une spectrographie de notre activité mentale, car elle n’est qu’un miroir ne nous révélant que les formes que nous-mêmes projetons, ici et maintenant, sur l’écran de la page où cette figure nous apparaît. Il s’agit donc d’une spectrographie tout à fait sui generis : car à la différence des figures (a) et (b), aucun pont interprétatif ne nous est nécessaire pour combler l’espace entre la trace spectrographique et la réalité effective de notre esprit, qui en elle se manifeste et s’auto-révèle grâce à la « voix muette » – la nôtre – retentissant dans nos oreilles internes.

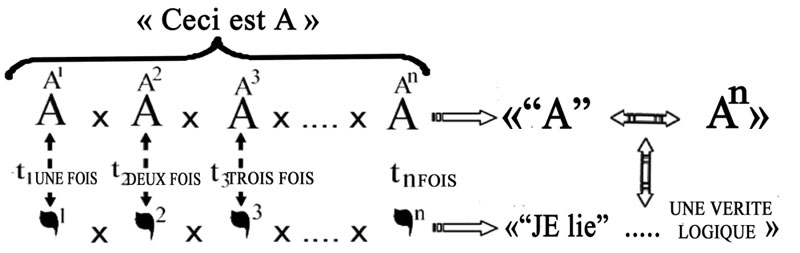
Figure 88 - Selon George Boole, l’évidence « A est A » – à savoir l’évidence du principe de non contradiction – s’exprime essentiellement dans le temps d’une réitération purement potentielle du jugement « ceci est A », que Boole mathématise en conséquence comme « An=A » (Loi des Index). En revanche, une réitération bien actuelle de ce même jugement a nécessairement lieu lorsque nous apprenons à lire « A », sans quoi nous ne pourrions atteindre aucune vérité mathématique. L’apparition de l’évidence « A=A » devant la conscience d’un enfant qui vient d’apprendre à lire est donc pensable comme la condensation de cette même suite d’apprentissage par récurrence, à l’intérieur d’une opération mathématique réalisée tout entière en un seul et même temps, à la fois potentiel (dans sa profondeur ) et actuel (sur sa surface).

Figure 89 [Galvani 1791. Table 1] - Galvani ressent donc le plein entre ces deux événements : « Frappé par la nouveauté de l’observation je fus saisi par une invincible curiosité et le désir d’expliquer le mystère du phénomène » [Galvani 1791]. Il le répète donc maintes fois pour s’en rendre certain, jusqu’à conduire sa demi-grenouille héroïque en présence de la Foudre [vis porcellosae, fulgurum fulminumque] pour voir si la foudre aussi, comme expression de notre entière existence planétaire, pouvait avoir cette influence à distance. Il a été confirmé en ses attentes, et depuis lors il n’a jamais abandonné son idée qu’une « électricité » irréductiblement « animale » existe, malgré la trouvaille révolutionnaire d’Alessandro Volta, lequel a rétorqué que l’électricité est partout. Ces deux positions sont évidemment vraies ensemble, car d’un côté il n’y a pas moyen de faire bouger nos jambes en chair et os si « the induced wires » de nos nerfs bien animaux ne sont pas actifs et vivants, mais de l’autre côté il est d’autant plus évident qu’un seul réseau d’une seule et même énergie (« un même courant » dit Ampère en ?323?) imprègne la totalité de ce qui bouge. L’obscure obsession « technologique » d’une époque toujours plus effrayée a ensuite opté pour la pensée généalogique la plus dévastatrice dont on puisse accoucher : comme une seule énergie est partout, on nivelle tout en bas, et on va chercher des piles, des tuyaux, des accumulateurs… où que nous trouvions un seul quantum de vie.

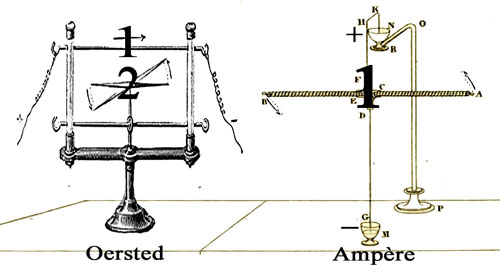
Figure 90 - Le solénoïde d’Ampère (à droite) est la condensation en un seul et unique phénomène de mouvement des deux phénomènes (électrique et magnétique) d’abord causalement liés par la découverte d’Œrsted.

Figure 91 (323) « Il faut distinguer deux sortes de conducteurs : 1° la pile même, […] 2° le fil métallique qui unit les deux extrémités de la pile. On peut comprendre ces deux cas dans une même définition, en disant qu'on entend par courant électrique la direction suivant laquelle l'hydrogène et les bases des sels sont transportés par l'action de toute la pile, en concevant celle-ci comme formant avec le conducteur un seul circuit […] Au reste, tout ce que je vais dire sur ce sujet ne suppose aucunement qu'il y ait réellement un courant dans cette direction, et on peut ne considérer que comme une manière commode et usitée de la désigner l'emploi que je fais ici de cette dénomination de courant électrique. » [Ampère 1820 : 197. L’italique est de moi. ]

Figure 92 - La « fovea » peut bien être comparée à la sphère circulaire purement dynamique qui entoure le centre de gravité/rotation de tout corps doué d’une inertie. -

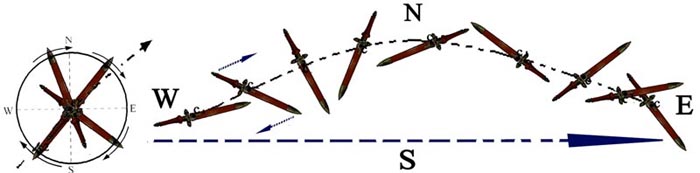
Figure 93 - Le sujet ultime du mouvement de chute qui anime un corps lancé dans l’espace, est sa « fovéa ».

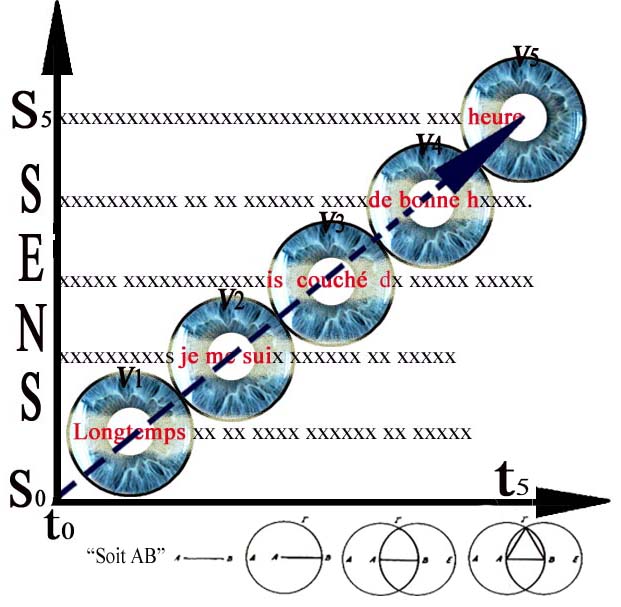
Figure 94 - (335) « La méthode de McConkie et Rayner, dite de la « fenêtre mobile », est plus modeste : elle permet de créer une illusion de texte sur un écran d'ordinateur. Elle consiste à équiper un volontaire d'un appareil de détection des mouvements de l'œil et à le coupler à un ordinateur de façon à modifier l'affichage du texte en temps réel. Ainsi peut-on programmer l'ordinateur pour n'afficher que quelques caractères de part et d'autre du point de fixation du regard, toutes les autres lettres de la ligne étant remplacées par des « x ». À titre d'exemple, la première phrase de À la recherche du temps perdu de Marcel Proust apparaîtrait ainsi :
Dès que le regard bouge, l'ordinateur rafraîchit l'écran afin de toujours présenter les lettres adéquates à l'endroit où l'on regarde, et des « x » partout ailleurs
xxxxxxxxs je me suix xxxxxx xx xxxxx.
xxxxxxxxxxxx xx xis couché dx xxxxx xxxxx
xxxxxxxx xx xx xxxxxx xxxxde bonne hxxxx.
xxxxxxxxx xx xx xxxx xxxxxx xx xxxne heure.
C'est ainsi que McConkie et Rayner ont fait une découverte remarquable et paradoxale : pour le sujet de l'expérience, cette manipulation est indétectable. Pour peu que l'on laisse suffisamment de lettres correctes de part et d'autre du point de fixation, le lecteur ne s'aperçoit de rien et croit avoir sous les yeux une page normale. En somme, il est aveugle dans une grande partie de son champ visuel et ne le sait pas. » [Ibid.]

Annexe I - De la "décharge" du reflexe aux mouvements évolutifs du sens

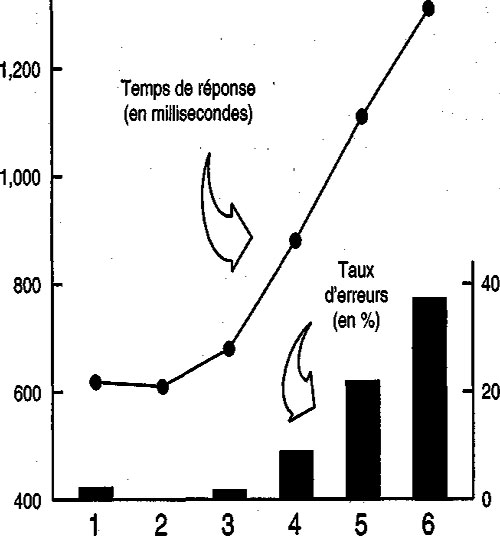
Figure A1 - La façon dont nos mouvements de réaction ralentissent suit deux lois : la « loi de taille » et la « loi de distance ». Ces deux lois qui régissent les accélérations/décélérations et l’orientation de nos mouvements nombrants montrent avec une évidence définitive que nous appartenons au même royaume numérique des rats, des pigeons et des nourrissons. Or ces deux lois réapparaissent apparemment identiques dans le monde irréversiblement symbolique du « 1, 2, 3» : c’est donc directement dans ce monde que je vais maintenant les prendre en considération.

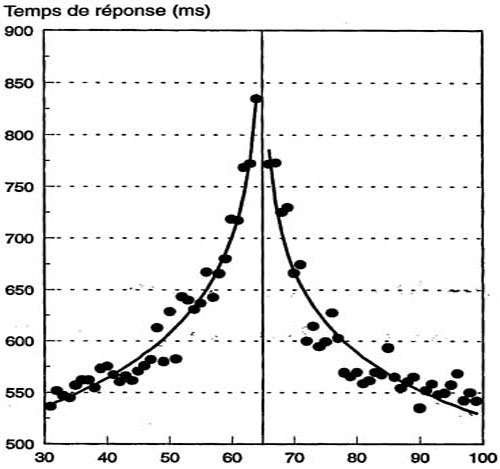
Figure A2 - Les variations de vitesse que subissent nos réactions musculaires selon le « poids » (taille/distance) des nombres qui nous frappent de « derrière » leur apparence perceptive, dessinent une parabole dynamique pleinement galiléenne. Il s’agit d’un mouvement « d'une régularité mathématique exceptionnelle » : une accélération continue et « sans à-coup », qui anime nos réactions en correspondance biunivoque avec la suite des nombres.

Figure A3ab [a) « Un enfant farceur a coupé en petits morceaux la ligne des nombres, en effaçant des chiffres. Récris les nombres qui manquent ». b) « Même la ligne du temps peut être représentée comme une ligne des nombres. Maintenant tu es en 2004. Écris les années précédentes et suivantes. » Lelli 2004, Vol.3]

Figure A 4 - Pour donner une capacité déterminante effectivement complète à notre suite « dextrogyre » DHG en Fig. A4, il faut ajouter que la même dictée orale alpha/aleph-bét/béithique « tracer un cercle “ABC ” » engendrera chez nos enfants un mouvement horaire [Fig. A4] tandis que les enfants israéliens dont parle Dehaene projetteront sur la feuille une rotation antihoraire, car pour eux aleph, beith, guimel...va de droite à gauche. Mais si c’est ainsi, alors les choses se renversent complètement. Si là derrière – beyond the signes – où selon Willian Rowan Hamilton habitent « the things signified » ((179) il n’y a aucune « raumliche Ding » (153) capable de donner un sens à notre écriture, alors nous devons rebondir sur ces mêmes signes, et reconnaître que le sens d’une écriture n’est rien d’autre – rigoureusement rien d’autre – que l’écriture d’un sens.

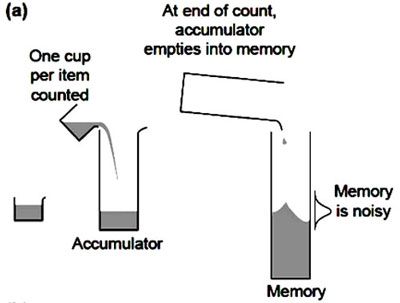
Figure A5 - Nous savons d’ailleurs que la « signature » de notre appartenance au royaume animal est dans les effets de « taille » et « distance » régis par la « Loi de Weber » qui dispose les erreurs de notre accumulateur sur une « échelle logarithmique » qui mathématiquement nous rend toujours plus incapables de maîtriser notre cognition mathématique. Cette circonstance est représentée par G & G avec les fluctuations de l’eau stockée dans le réservoir (« the sloshing in the beaker ») qui représente « the recalled magnitude », à savoir l’identité du nombre auquel nous ajoutons les autres au fur à mesure qu’ils s’accumulent. (A14) « The non-verbal counting process increments the accumulator by one ‘cup’ [ici- Fig. A5] for each item counted.The accumulation at the end of a count is read into memory. Magnitudes read from memory to serve as the targets in subsequent counting trials exhibit scalar variability, represented here by the sloshing in the beaker, which introduces noise into readings of the beaker (recalled magnitudes). » [Ibid.] - Nous reconnaissons facilement dans ce caléidoscope de « modèles » lourds et arbitraires, réfractés et multipliés sans limites par une imagination qui pense pouvoir tout faire et tout dire, la « mode de Londres » dénoncée il y a un siècle par Pierre Duhem (N17). La nature fictive de cette image maxwell/wienerienne est en somme évidente et explicitement admise, et ainsi que dans le cas de la perche d’Einstein, il n’y a pas moyen de compter les nombres grâce à des billes, sans présupposer le contraire.

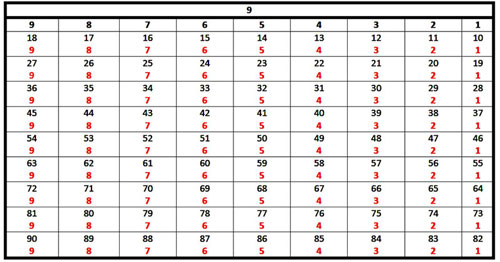
Figure A6 - Une quelconque table de comptage comme celle ci-dessus révèle de se déployer suivant une dimension de surface – où se succèdent les quantités, selon une pure et simple accumulation successive de leur « taille » – et une dimension de profondeur, où ce qui « compte » est au contraire l’identité numérique absolue des symboles qui composent les chiffres signifiant les nombres.

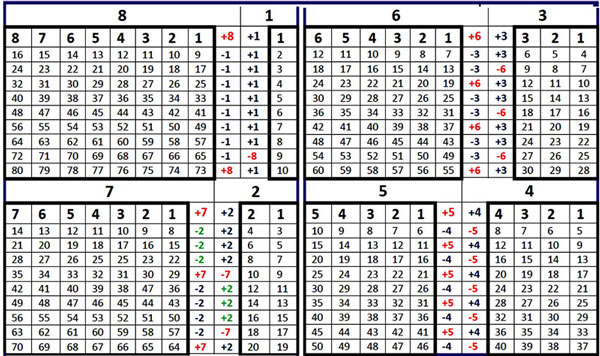
Figure A7 - Les différentes façons de se déployer d’une table de comptage selon le « module » choisi, montrent les inépuisables couches d’« harmonie arithmétique » qui composent l’identité vivante de l’« arbre des nombres »

Annexe II - De la combinaison à l'expression

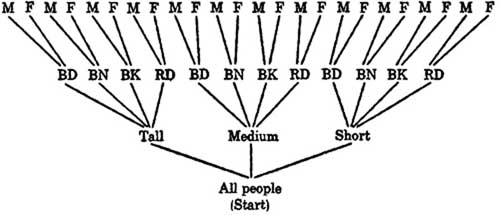
Figure A8 - Dans cet exemple, la possibilité logique ouverte par la proposition « cette personne (1) est une femme (1/2) blonde (1/4) de taille moyenne (1/3) » confère à sa vérité une mesure (une probabilité) de 1/24. Autrement dit : si ceci est 1 être humain, alors il y a 1 « sur » 2×3×4=24 possibilités que dans son cas se vérifie la circonstance « cette personne est une femme blonde de taille moyenne ». Le principe qui régit le découpage interne – diaïresis après diaïresis – d’un ensemble combinatoire de possibilités logiques, affirme donc que toute action mathématique r dirigée sur une autre action mathématique s a la nature d’une multiplication r × s.

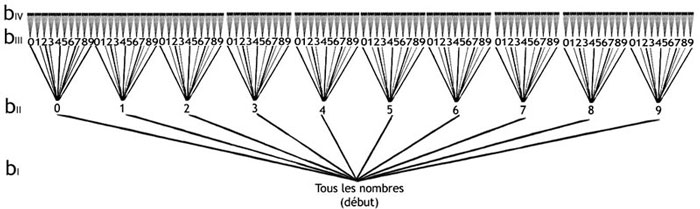
Figure A9 - [de moi] Aucun arbre combinatoire ne pourra jamais représenter la suite naturelle des nombres de façon mathématiquement rigoureuse, car les lois du calcul combinatoire sont, au contraire, rendues possibles uniquement par notre pré-connaissance des nombres, et pas l’inverse.

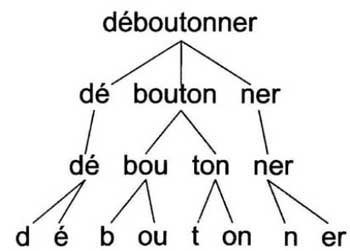
Figure A10 - « [1] Chaque mot est un arbre – En dépit des différences initiales, le système visuel du lecteur convergera vers la même représentation abstraite, l'essence même de la suite de lettres « DEUX », indépendamment de leur forme particulière – un code abstrait capable d'orienter le reste du cerveau vers la prononciation et le sens de cette chaîne de caractères. À quoi ressemble ce code abstrait ? S'agit-il juste d'une liste de lettres, D-E-U-X, sans structure particulière ? Non. [2] On s'oriente aujourd’hui vers l'hypothèse d'une représentation hiérarchique, où chaque mot écrit serait représenté par un arbre, dans lequel les lettres se regroupent en unités, elles-mêmes imbriquées dans des groupements de taille plus élevée – un peu comme un corps humain peut être représenté par l'agencement de ses parties, jambes, corps, tête, elles-mêmes constituées d'éléments plus simples. [3] Quelles sont donc les parties pertinentes d'un mot ? Disséquons ensemble le mot « déboutonner », par exemple. Nous y trouvons un préfixe « dé » et un suffixe « ner » qui encadrent et nuancent l'élément central, le mot au sein du mot, la racine « bouton ». Tous ces éléments s'appellent des « morphèmes » : ce sont les plus petites unités de sens que contiennent les mots. L'assemblage des morphèmes détermine le sens du mot. [4] Tout se passe donc comme si notre système visuel faisait un rapide pari sur la décomposition présumée du mot en morphèmes. Il dissèque le mot « baguette » en [bague]+[ette] en espérant que cela sera utile aux opérateurs suivants chargés d'en calculer le sens. » [Dehaene 2007 : 51. Les italiques et les crochets sont de moi.]

Annexe III - Les mirobolantes aventures du trait de plume

Figure A11

Figure

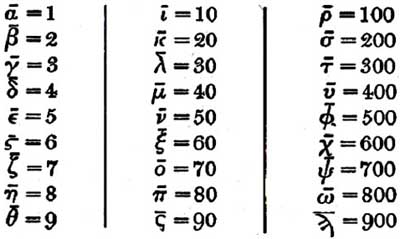
Figure A13 - "The horizontal stroke is often omitted for convenience in printed texts. In this system there are three letters (Stigma, a form of the digamma [le vav de Dhombres] Koppa [le 500] and Sampi [le 900] which had been taken over by the Greeks from the Phoenician alphabet but had dropped out of literary use. As there is no record of this alphabet of 27 letters in this order being in use at any time, it seems to have been deliberately framed by someone for the purposes of mathematics" [Goold 1980: 42-3. L’italique est de moi.]

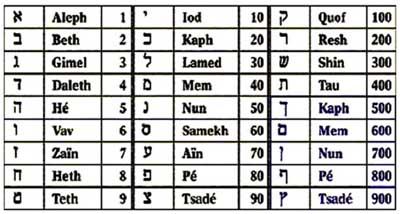
Figure A14 -La table en Fig. A13 nous donne des informations précieuses, si seulement nous l’enrichissons d’une autre table encore, qui démentit en effet les mots de M. Goold, selon lesquels « there is no record of this alphabet of 27 letters in this order being in use at any time ». Bien au contraire, cet alphabet existe, et c’est justement l’alphabet hébreu utilisé pour noter les nombres. Selon la « Gemutriah », à chaque lettre de l’alphabet on peut assigner un nombre qui lui correspond, et qui pourra être additionné (selon le critère utilisé dans l’épreuve par neuf) aux nombres correspondant aux autres lettres d’un même nom, pour identifier ainsi la « racine numérique » de ce nom.Si maintenant nous comparons les deux tables A13 et A14, nous reconnaissons que du point de vue purement graphique, le passage Ro(10)-->Qof(100) est aussi indéniable que le passage « Vav-->Vav », et on peut manifestement poursuivre dans cette direction une recherche aussi fertile que scientifiquement prometteuse, à tous les niveaux (le « Koppa » et le « Qoph » ont-ils une relation ?). Quant aux nombres, les deux tables répètent ma table en Fig. A6. Il est suffisant de les verticaliser (en sens horaire), pour voir que le passage d’une ligne à l’autre se fait de façon à garder la même « racine numérique » pour chaque colonne. La suite Aleph-->Yod-->Qof se présente donc comme les trois couches dimensionnelles d’une numération « base 10 » qui, de manière compréhensible, se limite à ces trois premiers pas si les savants qui l’ont conçue se meuvent orientés par la même intention euclidienne, que Jean Dhombres a si profondément cernée [cf.N36-37] : c'est-à-dire s’ils pensent que le nombre – ainsi que l’espace – n’a pas plus que trois dimensions. Dans ce cas, le Yod/Iota et le Qof/Ro seraient respectivement le carré et le cube de l’Aleph/Alpha.

Figure A15 - «La tradition chinoise, rapportée par le Livre des Mutations médite sur le Yin et le Yang, enclos dans des surfaces de même aire, délimitées par des arcs de cercle, le périmètre de chaque partie étant égal au périmètre total. Ce graphisme peut se multiplier par récurrence. » [Dhombres 1978 : 83]

Figure A16 En le traçant tout autour de ce « graphisme », j’ajoute, la tradition chinoise médite le Trait de Plume. Il est impossible de comprendre les processus de la médecine, des arts martiaux et finalement de toute la sagesse chinoise, si l’on ne se met pas en résonance avec l’identité purement expressive de ses 23 « combinaisons » graphiques que sont les 8 tri-grammes se succédant autour du « Taï-Chi », la sphère de tout ce qui existe, incessamment vivifiés par la respiration duale et galiléenne du Ying et du Yang. - La méditation taôiste et bouddhiste se focalise sur la façon dont la « multiplication par récurrence » impliquée par le « Tai chi » enchaîne les 64 [=26 arrangements-avec-répétitions] états fondamentaux de la Mutation. L’esprit/corps de l’homme qui médite les pakwa, transperce toutefois la surface de la combinaison/manipulation, afin que la combinaison/expression parle à ses oreilles, et libère ainsi les énergies bloquées de son être profond.